

Les représentations de l'énergie du vide spatial par les sciences physiques
Les phénomènes quantiques expliqués par
le champ du point zéro
électromagnétique classique
selon l'électrodynamique stochastique
Où l'on découvre que la quantification n'est pas nécessaire pour rendre compte de nombreux phénomènes dits quantiques - que la gravitation et la masse semblent être des manifestations du champ du point zéro
Alain Boudet
Dr en Sciences Physiques
 4. Le champ d'énergie de l'espace semi-classique
4. Le champ d'énergie de l'espace semi-classiqueRésumé: L'électrodynamique stochastique s'est développée à partir des années 1960 comme alternative à la physique quantique. Elle s'appuie sur l'électromagnétisme classique auquel elle adjoint la présence d'un champ d'énergie du vide. Par l'action de ce champ fluctuant sur les particules, elle rend compte de phénomènes habituellement considérés comme purement quantiques (l'indétermination de Heisenberg, la stabilité des orbites atomiques, l'intrication, etc.). Elle conserve les concepts familiers de causalité et de trajectoire, ce qui la rend attrayante et fluide. La constante de Planck y figure naturellement comme mesure de la densité énergétique du champ. Certains chercheurs ont même montré que les perceptions de masse, d'inertie et de force de gravitation pourraient résulter de forces de résistance induites par le champ du vide sur la matière. Cela ouvre une autre vision de l'univers où les formes de la matière résultent d'un équilibre susceptible d'évoluer.
Dans le premier article de cette série, j'ai décrit les principes de la physique classique qui ont été élaborés jusqu'à la fin du 19e siècle. Mis à part quelques phénomènes qui ne pouvaient pas être expliqués dans ce cadre, ces principes forment un ensemble cohérent: d'un côté la matière, constituée d'atomes et d'électrons, de l'autre les champs magnétique et électrique. Ils sont gouvernés par des lois qui sont tout aussi cohérentes: lois de Newton pour la matière, lois de Maxwell pour les champs. À cette époque, les champs sont décrits comme portés par une substance qui remplit l'univers, l'éther, mais on ne peut pas la mettre en évidence, et on ne sait pas comment la définir. C'est une option philosophique.
Puis dans le deuxième article, j'ai décrit les principes de la physique quantique et ses lois (quantification, élimination de la notion de trajectoire, intrication de particules distantes, abandon de la notion de réalisme). Cette physique a été élaborée dans un effort pour formaliser certains phénomènes qui étaient inexplicables dans le cadre de la physique classique. Elle s'est construite sur le concept d'un espace vide. L'éther en a été exclu, parce que superflu.
Enfin dans le troisième article, j'ai relaté comment les efforts pour concilier la physique quantique avec la Relativité Restreinte avaient conduit à l'élaboration d'une physique quantique des champs. La conséquence mathématique de cette association est l'existence d'un champ d'énergie quantique de l'espace, présent même à la température du zéro absolu: le champ du point zéro (CPZ). Il est en quelque sorte la résurgence du concept d'éther, avec un tout nouveau visage.
Puisque la physique quantique a réintroduit le champ du vide, on peut se demander s'il n'aurait pas été judicieux de le conserver dans le cadre de la mécanique classique, en redéfinissant ses caractéristiques physiques. En clair, au corpus de lois de la physique classique (lois de Newton et lois de Maxwell), on peut ajouter la présence d'un champ du point zéro qui obéit à ces lois classiques, et qui n'est pas quantifié. Puis on en calcule les conséquences mathématiques, et on les compare aux résultats expérimentaux connus.
C'est ce qui a été fait par une lignée de chercheurs qui ont construit une théorie alternative à la mécanique quantique: l'électrodynamique stochastique (ou SED - nom un peu rébarbatif pour le néophyte, dont j'expliquerai la signification très simple plus loin). Cette théorie a produit des résultats significatifs, qui ont permis de mettre en lumière ce qui, dans des phénomènes dits quantiques provient en fait de la présence du champ du point zéro.
En effet, ces chercheurs ont montré que des phénomènes que la physique classique ordinaire n'expliquait pas (spectre du corps chaud, indétermination de Heisenberg, etc.), recevaient une explication très simple dès lors qu'on suppose la présence de ce champ CPZ fait d'ondes électromagnétiques fluctuantes.
De plus, cette explication des phénomènes par la SED est fondée sur la représentation d'une réalité physique, contrairement à la physique quantique qui les constate mais ne sait pas les interpréter. Par exemple, dans la représentation de l'atome, la physique quantique abandonne l'idée que l'électron décrit une orbite autour du noyau, pour la remplacer par une probabilité de présence. Mais il reste que l'électron possède une énergie de rotation (moment cinétique) et qu'il devrait perdre de l'énergie et tomber sur le noyau. La physique quantique n'explique pas pourquoi il ne le fait pas. Elle dit simplement: on pose l'état de stabilité de l'électron sur son orbite atomique comme un fondement de la physique quantique. L'électrodynamique stochastique l'explique parfaitement, comme nous allons le voir plus loin.
Cette théorie alternative à la physique quantique a insufflé une nouvelle vision de la physique. Elle donne aussi des explications aux notions de masse, d'inertie et de gravité qui n'ont jamais été explicitées et pour lesquelles la physique classique ordinaire et la physique quantique restent muettes. Elle ouvre également la possibilité théorique de technologies innovantes de production d'énergie libre. Cela heurte les esprits, et cela pourrait expliquer qu'elle ne soit ni soutenue ni enseignée.
Malheureusement la théorie quantique s'est développée à la façon d'un rouleau compresseur. Elle occupe l'attention, le temps et l'argent des universités. L'électrodynamique stochastique n'a pas été prise en compte, sauf dans des exceptions locales. Parce que ses contributeurs ne se sont pas engouffrés dans le courant quantique, ils sont restés des cas à part, et l'histoire et l'actualité ne les ont pas mis en lumière. Il me tient donc à cœur de faire connaitre leurs travaux.
De façon générale, la physique s'efforce de décrire les mouvements de la matière sous l'effet des forces. Ces forces peuvent être représentées par des champs dynamiques, par exemple électrique, magnétique ou gravitationnel. Les variations dynamiques des champs sont décrites comme des mouvements d'ondes (voir article Matière et rayonnements).
Les forces ont une réalité incontestable, car chacun peut les ressentir et des appareils peuvent les mesurer. Mais qu'en est-il des champs qui les représentent? La question s'est posée et se pose à de nombreux savants de savoir s'ils ont une réalité physique ou s'ils sont seulement une écriture mathématique descriptive. Quelle que soit la réponse que donnent les philosophes, la physique contemporaine postule par définition que les champs sont des éléments fondamentaux constitutifs de l'univers.
La partie de la physique qui décrit les champs électromagnétiques s'appelle l'électrodynamique (ce mot signifie mouvements d'électricité). Elle étudie les mouvements des charges électriques (électrons et ions), et les champs électromagnétiques que ces charges produisent ou auxquels elles sont soumises.
L'électrodynamique a d'abord été élaborée dans le cadre de la physique classique. L'électrodynamique classique repose d'une part sur les équations de Newton et de Lorentz qui décrivent le mouvement des charges et d'autre part sur les équations de Maxwell qui décrivent les variations des champs électromagnétiques.
Puis s'est développée une électrodynamique quantique. Dans mon article précédent sur la physique quantique relativiste, j'ai défini ce qu'était l'électrodynamique quantique relativiste, appelée ensuite théorie quantique des champs électromagnétiques. Les transferts d'énergie entre matière et champs y sont quantifiés et les champs électromagnétiques sont eux-mêmes également quantifiés.
L'électrodynamique stochastique (SED) s'appuie sur l'électrodynamique classique et lui adjoint un éther constitué d'un ensemble statistique aléatoire de radiations électromagnétiques au point zéro (c'est-à-dire défini à la température du zéro absolu). Cette adjonction confère à la physique classique une nouvelle puissance explicative et prédictive. Stochastique signifie aléatoire ou régi par le "hasard", donc calculé selon les lois mathématiques statistiques des probabilités.
Dans l'article Concepts de la physique quantique, nous avons vu que le physicien allemand Max Planck (1858 - 1947) étudiait le spectre des rayonnements lumineux des corps chauds et tentait d'en rendre compte par une formule mathématique. D'autres avant lui l'avaient tenté et avaient produit des formules insatisfaisantes. Ainsi la formule de Rayleigh et Jeans fonctionne bien aux basses fréquences, mais elle prédit des énergies émises bien trop grandes dans le domaine des ultraviolets. En 1900, Planck parvint à trouver une formule qui rendait compte des résultats expérimentaux de manière satisfaisante.
Bizarrement pour l'époque, il avait dû, pour ajuster sa courbe mathématique aux résultats expérimentaux, y introduire une constante, la fameuse constante de Planck h. On comprenait cette introduction en faisant l'hypothèse que la matière chaude émettait ses radiations par paquets, et non de façon continue. Plus précisément, les radiations de fréquence f étaient émises en paquets d'énergie h.f .
Pour mieux comprendre la différence entre une émission continue et une émission par paquets, je propose l'image d'une roue à godets (noria) placée dans un courant d'eau. Elle recueille l'eau de la rivière dans des godets et déverse leur contenu dans un conduit de distribution. Elle déverse donc l'eau par quantités finies, le volume d'un godet. Pourtant cela n'implique pas que cette segmentation par quantités finies soit dans la nature même de l'eau qui reste un courant continu avant et après ce prélèvement.
 |  |
| Max Planck (1858 - 1947) Merci à Wikipedia | Une noria ou roue à godets, sur la rivière Regnitz, à Erlangen en Bavière, Allemagne. Merci à Wikipedia. |
De façon analogue, Planck ne considérait pas l'échange par quantités finies comme la quantification de la radiation elle-même par nature, et il faut insister sur ce fait peu connu. Il pensait que c'était juste le procédé employé par la matière. C'est Einstein en 1905 qui reprit l'idée des paquets d'énergie finie pour les placer au rang d'éléments constitutifs de la lumière elle-même (nommés photons par la suite), proposition qui sera le début de l'élaboration de la physique quantique.
Planck n'a jamais été un partisan de la quantification et il s'est opposé fortement au concept de grain de lumière. Son insatisfaction le poussa à creuser davantage la question et en 1911, Planck formula une seconde loi du rayonnement d'un corps chaud en équilibre thermique. Elle était une variante de la première. À la contribution en énergie de chacune des fréquences f, il avait ajouté un terme totalement indépendant de la température, qui subsiste au zéro absolu. En d'autres termes, il venait de montrer l'existence d'un champ d'énergie électromagnétique au point zéro. C'était un champ électromagnétique réel. Il le proposa comme alternative aux quanta de lumière.
En 1913, Bohr construisit son modèle de l'atome où les électrons tournent autour du noyau avec des niveaux d'énergie quantifiés. Dans la formule qui donne la valeur de l'énergie des niveaux, Bohr introduisit la constante de Planck h (voir article Concepts de la physique quantique). Comme sa théorie expliquait les séries des valeurs d'émissions spectrographiques des atomes, elle eut du succès. Ce succès s'étendit peu à peu jusqu'à conduire à l'élaboration de la théorie quantique des champs, de telle sorte que le quantique devint la voie obligée. La seconde loi de Planck fut négligée un certain temps, jusqu'à ce que les travaux de Planck soient redécouverts dans les années 50. À ce moment, certains chercheurs en comprirent l'intérêt et l'utilisèrent comme fondement d'une nouvelle théorie, l'électrodynamique stochastique (SED).
La SED est donc proche des propositions initiales de Planck en 1911. Alors que les physiciens considèrent que Planck est le père de la mécanique quantique, à cause de l'introduction de sa constante h, considérée ensuite comme l'unité de quantification, son attitude d'esprit était en réalité orientée vers le champ du point zéro dans le cadre de la physique classique, et il serait donc plutôt le père de l'électrodynamique stochastique.
L'électrodynamique stochastique s'est développée à partir des années 1960. Elle a été peu relayée par les journaux scientifiques, et dans ses débuts les quelques chercheurs qui travaillaient sur ce sujet de façon isolée n'étaient pas forcément mutuellement au courant de leurs travaux respectifs.

Pr. Timothy Boyer
Le premier à porter ses efforts dans cette recherche fut Trevor W. Marshall (physicien britannique). Puis Timothy Boyer (physicien états-unien, né en 1941) y contribua indépendamment. Par la suite, vers 1970 et jusqu'à récemment, d'autres ont poursuivi dans cette voie.
Ces chercheurs ont démontré que de nombreux phénomènes, décrits par la physique quantique comme résultant de la quantification de l'énergie et de l'indétermination de Heisenberg, peuvent en réalité être expliqués par cette théorie classique.
La théorie repose sur la physique classique et y ajoute la présence du champ d'énergie du point zéro. Elle aboutit à des équations semblables à celles issues du champ quantique, mais elle offre une interprétation physique bien différente. Contrairement à la physique quantique, elle ne remet pas en cause la notion de causalité ou de trajectoire d'une particule.
Toute théorie physique est définie par ses postulats de base, suggérés par l'expérience et teintés de philosophie, que l'on pose comme principes premiers indémontrables. À partir de ces postulats, on calcule les caractéristiques et propriétés de la matière et on vérifie qu'elles sont en accord avec l'expérience.
L'électrodynamique stochastique repose sur sa définition du champ du point zéro, une nouvelle version de l'éther, la substance invisible qui remplit le vide.
Depuis les débuts de la physique scientifique, les physiciens estiment que cette substance a une existence réelle. Quand les concepts de champs magnétiques et électriques ont été élaborés, l'éther était conçu comme le support matériel de ces champs. De même que l'eau est le support matériel des vagues, de même l'éther était imaginé comme le support des ondes électromagnétiques qui se propagent et transportent de l'énergie. C'était la pensée de Robert Hooke, de Huygens, Fresnel, Maxwell...
Mais cet éther imaginé n'était pas inclus et formalisé dans la théorie. Il restait une image philosophique suggérée par l'analogie avec l'eau. On en décrit les vagues (les ondes de lumière), sans avoir besoin de définir ce qu'est l'eau (l'éther). Ceux qui ont tenté de préciser sa nature et ses propriétés s'y sont cassé les dents. À l'image de l'eau, ils supposaient que ce fluide avait des caractéristiques matérielles. Aussi, calculaient-ils, compte tenu de la vitesse de propagation de la lumière dans l'éther, l'éther doit être plus rigide que l'acier. Mais c'était incompatible avec l'observation des astres qui n'auraient pas pu se déplacer dans cet éther rigide.
Par contre, si on envisage un éther sans propriétés matérielles, on aboutit à un ensemble explicatif cohérent. C'est le cas d'un champ fait de radiations électromagnétiques, comme celui de l'électrodynamique quantique et celui de l'électrodynamique stochastique.
L'éther postulé par l'électrodynamique stochastique (ou champ électromagnétique classique du point zéro) est constitué d'un bain de radiations électromagnétiques de toutes les fréquences, des plus basses aux plus hautes, en équilibre à la température de 0°K. C'est un éther physique réel, pas une abstraction mathématique.
Selon Timothy Boyer (voir Boyer 2011), ce spectre doit être doté de certaines qualités: homogène dans tout l'espace, isotrope (le même dans toutes les directions), et invariant dans un changement d'échelle (il est le même dans un tout petit espace ou dans un immense espace). De plus, ce champ doit respecter les lois de la Relativité Restreinte (il doit être invariant dans la transformation mathématique des formules de Henrik Lorentz).
En imposant ces conditions mathématiques, Boyer trouve qu'un seul type de distribution de fréquences peut les satisfaire: l'énergie de chaque fréquence à 0°K est proportionnelle à la fréquence (E0=C.f).
Il reste cependant un facteur multiplicatif indéterminé, C. Nous verrons un peu plus loin que des mesures expérimentales ont permis de déterminer sa valeur. Il est égal à h/2. Avec cette valeur, on retrouve précisément le champ de la deuxième formulation de Planck.
À partir de cette définition mathématique de l'éther à 0°K, on en calcule les conséquences. Que devient-il si on augmente la température? Retrouvons-nous le spectre de rayonnement de Planck? C'est effectivement le cas.
Boyer fait remarquer que cet accord avec la formule de Planck est obtenu seulement si on tient compte de la Relativité Restreinte. Dans le cas contraire, le calcul aboutit à la formule classique ancienne (rayonnement dit de Rayleigh-Jeans) qui n'est pas en accord avec les mesures.
C'est pourquoi le champ du point zéro de l’électrodynamique stochastique s'inscrit dans le cadre de la Relativité Restreinte.
La SED, tout comme Planck, postule que le champ du point zéro a une existence réelle. Dans ce cas, il devrait être possible de le mettre en évidence expérimentalement.
Michelson et Morley avait tenté de mettre l'éther en évidence au moyen d'un interféromètre, comme j'ai l'ai rapporté dans l'article précédent. Leurs résultats ont été négatifs. Mais à leur époque (un peu avant 1890), ils imaginaient un éther immobile dans l'espace comme un lac un jour sans vent. La Terre s'y meut comme un bateau sur le lac, et ils pensaient pouvoir détecter un vent d'éther.
Par contraste, le champ du point zéro de la SED est animé de mouvements fluctuants. Puisqu'il est relativiste, son spectre de fréquences est identique dans des repères se déplaçant à vitesse constante l'un par rapport à l'autre. Si cette description est juste, alors les expériences de Michelson et de Silvertooth étaient vouées à l'échec, puisque la Terre avance à vitesse constante par rapport à l'espace en première approximation.
Est-ce à dire qu'on ne peut pas mettre le champ en évidence? On le peut si la vitesse relative de deux repères (liés à deux objets par exemple) n'est pas constante, autrement dit si l'un est accéléré par rapport à l'autre. Dans ce cas, la distribution spectrale des champs observés dans les deux repères change d'allure et on devrait pouvoir détecter ce changement.
Le physicien canadien William G. Unruh (né en 1945) et le physicien britannique Paul C.W. Davies (né en 1946) ont calculé chacun indépendamment que dans un mouvement accéléré uniformément, le spectre du champ CPZ prend l'apparence du spectre d'un corps chaud (effet Davies-Unruh). Toutefois, une accélération extrêmement élevée est requise pour obtenir une augmentation de température de seulement 1°K, et il y a peu de chance de pouvoir la détecter expérimentalement.
Il existe une autre voie pour modifier le spectre du CPZ, c'est de le confiner dans une cavité suffisamment petite pour que les longues ondes (basses fréquences) n'aient pas la possibilité de s'y déployer. À cause de ce déséquilibre en fréquences, le physicien néerlandais Hendrick Casimir (1909 – 2000) a prévu par le calcul en 1948, dans le cadre de l'électrodynamique quantique, que deux plaques métalliques placées parallèlement dans l'espace à très petite distance à la température du zéro absolu doivent subir une force qui tend à les attirer l'une vers l'autre. Je l'ai décrit en détail dans l'article précédent.
Diverses expériences ont été réalisées pour mesurer cette force à très basse température, en particulier celles du physicien états-unien Steven Lamoreaux, en 1996, suivies par d'autres. Les mesures concordent avec les prévisions mathématiques de Casimir. La force ne s'annule pas lorsque la température s'approche de 0°K. En fait elle devient indépendante de la température. Ces résultats ont été interprétés comme la confirmation de la réalité du vide quantique et de la validité de la quantification de l'énergie des radiations électromagnétiques.
Or Boyer a démontré que la force mesurée entre des plaques conductrices proches était tout aussi bien en accord avec les prédictions de l'électrodynamique stochastique, sans quantification.
En conséquence, la force de Casimir est l'indice de la réalité du champ du point zéro.
C'est en comparant la valeur fournie par la mesure expérimentale de la force de Casimir avec sa valeur prévue par son calcul en SED que Boyer en a déduit la valeur du facteur C du CPZ cité plus haut. Cette valeur se trouve être exactement la constante de Planck h divisée par 2.
La valeur de la constante C est déterminée à 3,31 x 10-34 Joule x seconde.
La constante h prend donc un statut bien différent de celui qu'elle a en physique quantique. C'est celui que Planck lui a donné à l'origine. Elle ne fait pas figure d'un quantum d'action, ni d'une constante absolue, elle apparait comme un facteur d'échelle. De la même façon qu'on peut représenter un territoire sur une carte à une échelle arbitraire sans changer la nature de la carte mais en changeant sa taille, de même, la constante h fixe l'échelle des énergies du champ du point zéro.
E0=
Puisque la "constante" h est donc déduite des mesures expérimentales, est-elle vraiment une constante absolue de l'univers? Impossible de le dire. Ce qu'on constate, c'est que sa valeur représente la condition actuelle de notre Univers. Rien n'empêche de penser qu'elle puisse évoluer dans le temps ou avoir une valeur différente dans des espaces où les conditions du champ du point zéro sont différentes. Qui sait?
Si l'on admet l'existence d'un champ de radiations qui remplit l'espace, se pose alors la question de savoir d'où proviennent ces radiations. Y a-t-il des sources qui les produisent et si oui lesquelles?
Selon l'opinion de certains scientifiques, toute radiation est forcément produite par une charge électrique en mouvement accéléré (linéaire ou en rotation). En conséquence, les radiations sont produites par l'ensemble des charges électriques en mouvement de l'Univers. Réciproquement, ces charges subissent le champ qu'elles créent, en une boucle rétroactive. Ce point de vue a été conforté par des calculs du physicien états-unien Harold E. Puthoff en 1989 (Phys. Rev. A, 4857), en partant du modèle cosmologique inflationnaire.
Il est une variante du principe avancé par le physicien autrichien Ernst Mach (1838 - 1916) pour qui l'inertie d'un objet matériel dans l'univers serait induite par l'attraction de l'ensemble des autres masses présentes dans l'univers.
Mais selon d'autres scientifiques, ces radiations seraient présentes depuis l'origine de l'univers, plus exactement depuis le Big Bang, alors qu'aucune particule de masse, ni aucune charge électrique n'existaient. C'est ce que leur suggère l'existence du rayonnement dit fossile de l'univers supposé être un résidu du Big Bang. Autrement dit, les radiations appartiendraient de facto par nature à l'univers tel qu'il a été créé.
Le principe d'indétermination de Heisenberg est l'un des fondements essentiel de la mécanique quantique. Il énonce que si on mesure précisément la position d'une particule, on ne peut pas déterminer sa vitesse, et inversement. Ou bien, de la même façon, il y a un choix à faire entre déterminer précisément l'énergie de la particule et l'instant où on la détermine (voir article Concepts de la physique quantique).
Ce qui est étrange dans ce principe, c'est que le processus de la mesure, qui est un procédé pratique non inclus dans la théorie, intervient dans l'explication de cette théorie. Selon lui, on ne peut décrire le monde que par la mesure pratique qu'on en fait. La physique quantique renonce à décrire une réalité sous-jacente, non perçue. Elle renonce même à se poser la question de l'existence de cette réalité.
Au contraire, la SED affirme qu'il existe une réalité définie. Elle rend compte tout aussi bien de cette indétermination à cause du caractère statistique du champ du point zéro. La matière baigne dans le champ du point zéro qui agit sur elle comme un bruit de fond aléatoire. Il provoque des fluctuations de la position et de l'énergie de cette matière, par exemple une particule. D'où une certaine indétermination. L'indétermination n'est pas intrinsèque à la matière elle-même, elle résulte des interactions de la matière avec le champ du point zéro.
Le système de la particule doit donc être traité comme un ensemble statistique d'états fluctuants. Boyer a calculé que les valeurs prises par l'énergie et la position d'une particule chargée plongée dans le CPZ fluctuent exactement dans la fourchette d'écart prévue par l'indétermination de Heisenberg. L'électrodynamique stochastique constitue donc une explication alternative à l'indétermination, certainement bien plus simple et plus concrète que celle de la mécanique quantique.
On comprend aussi que ces fluctuations de la position d'une particule rendent illusoires les tentatives pour déterminer sa trajectoire précise. Cela n'empêche pas que cette particule obéit à la loi de la causalité, au même titre qu'une molécule dans un gaz soumise aux chocs avec les autres molécules. La physique quantique a abandonné la causalité et cela a tourmenté de nombreux esprits et fait couler beaucoup d'encre. C'est simplement parce qu'elle ignore l'influence du champ du vide responsable de cette indétermination.
Portons maintenant notre attention aux phénomènes que la SED a été capable d'expliquer. Celui du mouvement de l'électron en orbite dans l'atome est l'un de ses grands succès.
Après les expériences de Rutherford (physicien néo-zélandais, 1871 - 1937) sur la diffusion des rayons d'hélium par des atomes (voir article Concepts de la physique quantique), la physique classique se représente l'atome comme un petit système solaire, avec des électrons de charge négative qui tournent en orbite autour d'un noyau central à charge positive. Mais ce modèle n'est pas cohérent et pose un gros problème. Car selon les lois de l'électrodynamique classique, lorsqu'une charge électrique telle qu'un électron tourne, donc subit une accélération au sens mathématique (car sa vitesse est modifiée en orientation), elle émet un rayonnement électromagnétique, donc une énergie. Autrement dit l'électron perd de l'énergie continuellement. Or son énergie est celle de son mouvement de rotation. Cela indique qu'il ralentit, sa force centrifuge diminue et en conséquence il se rapproche du noyau. Aussi, selon l'électrodynamique classique, l'atome ne serait pas stable. Pourtant les observations expérimentales montrent qu'il l'est. Comment peut-on expliquer cette stabilité?
L'atome selon la représentation de Bohr
En 1913, Bohr supposa tout simplement que les niveaux d'énergie des électrons étaient quantifiés par nature, et qu'ils conservaient leur énergie sur une orbite sans rayonner. C'étaient les prémisses de la théorie quantique. Il ne pouvait donner aucune explication à ce fait, il disait simplement, "c'est comme ça selon la nouvelle physique atomique, c'est la nouvelle règle".
Or l'électrodynamique stochastique apporte une réponse beaucoup plus satisfaisante. Pour elle, il est inutile de poser une nouvelle règle. Il est inutile de quantifier les niveaux d'énergie de l'atome. La stabilité de l'atome est due à l'action du champ du point zéro.
Selon la SED, l'électron sur son orbite rayonne effectivement de l'énergie, selon les lois électromagnétiques classiques. Mais l'atome n'est pas isolé, car il est plongé dans le champ CPZ et il reçoit constamment de l'énergie de cette source. Aussi, l'électron gagne de l'énergie par ses échanges avec le champ du point zéro. Un équilibre se produit entre la perte et le gain, de sorte que l'atome est stable.
La vérification mathématique de cet équilibre a été effectuée par Cole et Zou en 2003. Ils ont constaté que le calcul de l'énergie de la particule en orbite n'aboutit à un équilibre que dans le cadre de la Relativité Restreinte. Les calculs de l'absorption d'énergie provenant du champ du point zéro furent repris selon une autre méthode par H.E. Puthoff avec le même succès.
Un support théorique a ensuite été développé par Peña et Cetto (2005), montrant comment l'effet de quantification nait de l'équilibre énergétique. L'équilibre ne se produit que pour certaines orbites. Les orbites qui sont retenues dans la quantification de la mécanique quantique correspondent à celles qui résistent aux perturbations provoquées par les fluctuations du champ du vide.
La physique quantique décrit les atomes comme ayant des caractéristiques fixes, avec des orbites aux niveaux d'énergie quantifiés déterminés. La série de ces niveaux est en quelque sorte leur fiche d'identité. Or s'il se révèle que ces niveaux d'énergie ne sont pas absolument intrinsèques, mais résultent d'un équilibre délicat avec l'environnement du CPZ, cela révolutionne notre vision de l'univers. On imagine qu'il suffit que le champ soit modifié pour que l'équilibre soit déplacé.
Imaginons que quelque part dans l'espace ou dans le temps, pour une raison technique ou cosmique, la densité d'énergie du champ se met à varier. Alors, toutes les structures atomiques seraient réajustées. Rappelons-nous que la valeur de cette densité globale du champ est indiquée par la valeur de la constante de Planck h, qui est un facteur d'échelle de ce champ. Si la valeur de h baissait, les fréquences d'émission lumineuse des atomes se décaleraient vers le rouge.
Cela pourrait être en rapport avec le décalage vers le rouge des émissions des étoiles, systématiquement interprété comme le signe que l'étoile s'éloigne de nous. Ne pourrait-il pas aussi être expliqué par la baisse de densité énergétique du champ du point zéro au voisinage de l'étoile?
Lorsque deux molécules sont proches l'une de l'autre, différents types de forces peuvent s'exercer entre elles. Si elles sont chargées électriquement, une force électrique se manifeste, qui les rapproche ou les repousse selon les signes contraires ou identiques de leurs charges. Si la molécule n'est pas chargée, donc globalement électriquement neutre, elle est cependant constituée d'atomes qui renferment des noyaux électriquement positifs et des électrons négatifs. La répartition de ces charges électriques dans le volume de la molécule est mouvante et à un instant donné le centre des charges négatives n'est généralement pas au même endroit que le centre des charges positives. La molécule est dite polarisée (sous forme de dipôle ou de multipôle). Deux molécules polarisées proches exercent l'une sur l'autre des forces électriques faibles appelées forces de Van der Waals.
Selon les enseignements académiques, les forces de Van der Waals ne peuvent être comprises que dans le cadre de la physique quantique. Mais Boyer démontra en 1973 que l'électrodynamique stochastique peut parfaitement en rendre compte. En effet, lorsqu'on place un atome dans le bain de radiations du champ du point zéro, il modifie la répartition des fréquences de ces radiations à cet endroit. Un autre atome placé à côté subit cette modification. Réciproquement ce deuxième atome modifie aussi le champ, et cette modification agit sur le premier. Ce sont ces modifications locales du champ du point zéro dues à la présence des atomes qui produisent des forces mutuelles sur les atomes appelées forces de Van der Waals.
Lorsque une onde de lumière se propage dans le champ du point zéro, elle interagit avec les ondes électromagnétiques constitutives de ce champ. Ces interactions la ralentissent, d'autant plus que l'interaction est forte. La lumière aurait donc une vitesse qui varie en fonction de la composition du champ du point zéro.
Serait-ce en contradiction avec la supposition que la vitesse c de la lumière est la même dans tout l'univers? On peut penser que non, puisque la SED postule que le champ est défini par une composition en fréquences et une densité précises. Alors les interactions sont les mêmes partout, ainsi que la vitesse de la lumière.
Toutefois, les caractéristiques du champ sont-elles immuables? La constante de Planck est-elle vraiment une constante? La distribution spectrale est-elle toujours celle qui est postulée dans la théorie?
On sait qu'il peut arriver des circonstances où le champ CPZ est modifié par une cause extérieure. C'est le cas dans l'espace compris entre les plaques de Casimir, où il y a absence d'ondes de grandes longueurs. On doit donc s'attendre à ce qu'entre ces plaques la lumière ait moins d'interactions et que sa vitesse soit plus grande que c (G. Barton, 1990, Phys. Lett. B, 237, 559).
Cela pourrait aussi arriver dans le cosmos. Puisque la présence de matière distord le champ du vide dans son voisinage, la vitesse de la lumière pourrait être modifiée au voisinage de certaines étoiles ou du soleil. C'est ce que pense l'astrophysicien états-unien Bernhard Haisch (nous relaterons plus loin ses recherches). Il décrit le champ du vide comme un milieu réfractant, qui dévie le trajet de la lumière à la manière du verre. L'indice de réfraction d'un milieu réfractant (qui reflète la grandeur de la déviation du rayon lumineux) est directement relié à la vitesse de la lumière dans ce milieu.
La déviation de la lumière à proximité d'une étoile a été mise en évidence et c'est un phénomène bien connu. Mais il est mis sur le compte des forces de gravitation comme prévu par les lois de la Relativité Générale. Haisch avance que la déviation du trajet lumineux au voisinage d'une étoile pourrait être causé par un changement de composition spectrale du champ.
Car au fond que savons-nous réellement de ce champ non encore exploré, mis à part ce qu'en suggèrent les mesures de la force de Casimir? Que savons-nous de l'évolution du champ du vide dans des espaces lointains ou sur de longues périodes? Pratiquement rien.
Par ailleurs on peut se pencher sur les bases expérimentales qui ont amené les physiciens à considérer que la vitesse de la lumière a une valeur constante bien définie qui semble éternelle.
Le chercheur australien Barry Setterfield, en collaboration avec Trevor Norman de l'Université Flinders (Australie), a fait des relevés minutieux qui ont révélé que la vitesse de la lumière décroissait lentement depuis qu'on a recueilli des mesures fiables, c'est-à-dire depuis 1870 environ. Cela est-il l'indice que le champ du point zéro aurait évolué?
La publication de Setterfield et Norman sur ce sujet en 1987 (The Atomic Constants, Light, and Time) contrariait aussi bien les adeptes de la théorie darwiniste de l'évolution de la terre que ceux de la théorie de la création divine terrestre il y a 6000 ans. Elle fut violemment critiquée et les publications ultérieures de ses auteurs furent refusées. Pourtant la même année 1987, indépendamment, le russe V. S. Troitskii publia des données qui montraient que la vitesse de la lumière était beaucoup plus grande dans le passé. Telle est la prétendue sagesse scientifique désintéressée !!
Les comportements des scientifiques dans les situations de controverse se reproduisent, fondés plus souvent sur les impulsions ou résistances émotionnelles des égos que sur des raisonnements objectifs (voir article Matière et rayonnements). Car cette histoire rappelle fortement les querelles qui eurent lieu lorsque l'astronome danois Roemer suggéra en 1676 que la vitesse de la lumière n'était pas infinie comme on le pensait auparavant avec Aristote, Descartes et Cassini, mais qu'elle avait une valeur finie. Cela prit un quart de siècle pour que les savants acceptent cette possibilité.
La physique quantique est connue pour avoir énoncé des principes qui remettent en cause le sens commun sur les notions de trajectoire, de déterminisme et de causalité (voir mon article Concepts de la physique quantique à ce sujet). Jusqu'à alors, il allait de soit qu'un corps était en mouvement sous l'effet d'une cause, et que sa trajectoire était déterminée par les caractéristiques de ce corps et les actions extérieures exercées sur lui. La physique quantique a remplacé ces notions par des probabilités de présence. De plus elle a inventé le concept d'états superposés, combinaison des états possibles d'une particule ou d'un ensemble de particules.
Il en résulte des situations très étonnantes comme l'état d'intrication d'un ensemble de deux particules. Lorsque deux particules (photons) ont été produites par une origine commune, par exemple émises en même temps par le même atome, leur avenir est lié par une intrication (états entremêlés) de telle sorte que si on agit sur l'une, l'autre réagit aussi immédiatement, même sans cause visible. C'est du moins l'interprétation donnée aux résultats de mesure statistique de quelques rares expériences.
Si l'on garde la vision de la physique classique, ce qui dérange dans le phénomène d'intrication est que l'influence d'une particule sur l'autre ne peut se faire que par une cause, un signal qui se propage de la première à la deuxième. Dans le cas de deux photons, cela voudrait dire que ce signal voyage de l'un à l'autre à vitesse infinie. Mais la physique incorpore comme une certitude les lois de la Relativité Restreinte, donc les signaux ne peuvent pas voyager à une vitesse infinie, mais à une vitesse maximum c. Alors comment expliquer le phénomène d'intrication qui est immédiat? La physique quantique ne l'explique pas, elle le calcule.
La SED en rend compte d'une façon simple et transparente. Ce qui apparait en physique quantique comme une intrication résulte en SED de corrélations entre les ondes électromagnétiques du champ du point zéro. Par exemple, considérons deux charges oscillantes couplées pour une raison quelconque (Emilio Santos, 2014). Chacune induit des variations dans le champ du point zéro. Ces variations sont corrélées et c'est cette corrélation qui apparait en physique quantique comme une intrication.
Pour Marshall, le concept d'intrication est inutile en SED. En physique quantique, il est seulement le prix qu'elle doit payer pour rester fidèle à son principe de quantification de la lumière sous la forme du photon.
Nous constatons que l'électrodynamique stochastique, fondée sur le champ du point zéro électromagnétique classique et sur les équations de Maxwell et de Lorentz (qui expriment la force qui s'exerce sur une charge), donne, au moins sur certains points, des résultats mathématiques analogues à ceux de l'électrodynamique quantique, fondée sur le champ du point zéro quantique et sur les lois de la mécanique quantique (équation de Schrödinger, indétermination de Heisenberg).
C'est vrai en particulier pour le spectre de rayonnements des corps chauds, la relation d'indétermination de Heisenberg, les orbites de l'électron de l'hydrogène, et l'équation de Schrödinger. Dans ce cas, quel avantage avons-nous à la prendre en considération? Que nous apporte-t-elle de plus dans la compréhension de l'univers? Doit-elle remplacer la mécanique quantique?
C'est la question que soulevait Nelson en 1966 dans une publication intitulée Derivation of the Schrödinger equation from newtonian mechanics (Phys. Rev. 150, 1079): Dans cet article, nous allons tenter de montrer que le changement radical de voie produit par l'introduction de la mécanique quantique par rapport à la physique classique il y a 40 ans n'était pas nécessaire. Nous donnerons une démonstration et une interprétation entièrement classique de l'équation de Schrödinger, en suivant une ligne de pensée qui est un développement naturel de raisonnement utilisé en mécanique statistique et dans la théorie du mouvement brownien.
Notre esprit a du mal à accepter les lois quantiques posées en tant que fondements mathématiques abstraits, sans que nous puissions imaginer un mécanisme concret sous-jacent. En contrepartie, l'avantage de l'électrodynamique stochastique est qu'elle apporte un éclairage essentiel sur l'origine des phénomènes. Elle reconstitue les mêmes lois avec des mécanismes réalistes qui nous sont familiers en physique classique. Les atomes et les particules ont des trajectoires définies, mais elles sont fluctuantes sous l'effet du champ du point zéro. Ce champ invisible est omniprésent dans l'univers et il contrôle la matière qui s'y trouve.
C'est un changement radical de notre vision de l'univers.
Toutefois, il reste des points que la SED n'a pas été en mesure d'élucider, là où la physique quantique apporte une réponse.
Il faut toutefois remarquer que le nombre de travaux consacrés à la SED est dérisoire par rapport à ceux consacrés à la physique quantique, qui aspire une part de budget importante. Elle demande à être perfectionnée, complétée, en particulier, dans la définition du champ du vide. En effet, on n'y a considéré que sa composante électromagnétique. Peut-être faudrait-il lui adjoindre d'autres caractéristiques?
Par exemple, nous verrons dans un autre article que l'univers n'est pas fait seulement d'ondes oscillantes. Elles sont animées de rotations et de mouvements spiralés (voir article Spirale, mouvement primordial de vie), qui s'expriment par exemple dans le spin des électrons et aussi sous forme de champs de torsion.
Puisqu'un ensemble de phénomènes est traduit formellement aussi bien par l'électrodynamique quantique que par l'électrodynamique stochastique, on peut se demander laquelle de ces deux théories REPRÉSENTE le mieux la réalité de l'univers physique.
En premier lieu, il est indispensable de garder à l'esprit qu'une théorie n'est pas une réalité. Elle est seulement un modèle possible pour décrire des phénomènes observés. Il en est ainsi de toutes les théories de la physique. Elles sont basées sur des principes (postulats) et sur des lois, posés comme tentative de rendre compte des observations.
Lorsque deux modèles théoriques rendent compte de certains phénomènes aussi bien l'un que l'autre, comme la SED et la mécanique quantique, comment déterminer si l'un est plus vrai ou plus plausible que l'autre?
Une démarche possible est de choisir le modèle qui semble le plus simple, le plus esthétique. C'est une option philosophique à laquelle les scientifiques font assez souvent appel parce qu'elle résonne avec notre cœur. Nous sommes attirés par l'image d'un monde harmonieux. Elle est habituellement nommée le rasoir d'Okham, du nom d'un philosophe anglais du 13e siècle.
Une autre démarche est de calculer les conséquences mathématiques et physiques de chacun des modèles. On va en particulier calculer comment le système évolue lorsqu'on fait varier une de ses variables. Cette évolution peut différer de façon sensible selon les modèles. On va ensuite effectuer des expériences pour comparer leurs prévisions, si tant est que ces expériences soient pratiquement réalisables, ce qui n'est pas toujours le cas.
L'électrodynamique stochastique a prévu des phénomènes en optique cristalline qui ont été vérifiés par la suite.
Selon l'interprétation quantique, l'onde entrante est faite d'un ensemble de photons. Dans le cristal, chaque photon est transformé en deux photons de fréquences f et f0-f inférieures à f0 (conversion diminuée), de telle sorte que dans l’assortiment des photons sortants, ils sont appariés deux par deux.
Dans l'interprétation de la SED, c'est une onde continue qui aborde le cristal. Elle se superpose au champ du point zéro qui imprègne tout l'espace, y compris l'intérieur du cristal. Des interférences se produisent entre l'onde entrante f0 et les ondes du champ f. Le rayon d'interférence est dévié et sort selon un angle qui dépend de la fréquence. Ce phénomène persiste même si l'intensité de l'onde entrante est quasiment nulle, car les ondes du champ du point zéro sont encore présentes.
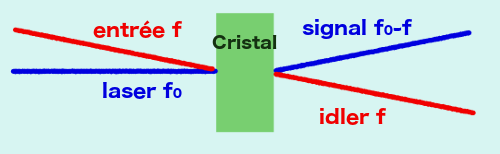
Un cristal de transparence non linéaire reçoit l'onde incidente d'un laser de fréquence f0. Si une onde du champ du point zéro, de fréquence f, est incidente selon un angle θ, un signal de fréquence f0-f est émis dans une certaine direction conjuguée. Ce signal sortant est appelé idler (signal lâche).
Or la SED prévoit un phénomène supplémentaire. Marshall (2002) a montré que les ondes du champ peuvent aussi donner lieu à des fréquences augmentées (f0+f) qui produisent un deuxième arc-en-ciel. Cette prédiction a été testée en 2009 et 2010 avec des résultats positifs, confirmant ainsi la validité de la SED, c'est-à-dire en particulier de la présence d'un champ électromagnétique classique du point zéro. Marshall conclut: De cette façon, nous sommes capables de comprendre, de façon complètement classique, le processus physique réel qui se produit dans le cristal.
Le champ d'énergie du point zéro est une réalité physique. C'est du moins ce que nous laisse penser la mise en évidence expérimentale de la force de Casimir. Il entre en interaction avec les particules de matière qui y sont placées, et donne lieu à différents phénomènes comme les forces de Van der Waals.
Poussant plus loin les conséquences de ces interactions, certains chercheurs ont proposé que les perceptions de masse et d'inertie pouvaient en être le résultat. Cela bouscule toutes les représentations de la physique classique à ce sujet, qui considère que la masse est une caractéristique propre à l'objet lui-même, indépendante de son environnement.
Nous sommes habitués à penser que la masse d'un objet est une caractéristique naturelle de l'objet lui-même. En effet, lors d'échanges commerciaux, on évalue le prix de certaines denrées par leur quantité. Mais en réalité, on mesure cette quantité sur une balance, donc par son poids. Ainsi, dans notre quotidien, il y a identification entre le poids et la quantité de matière. Or ce sont deux notions différentes.
Le poids d'un objet est perçu comme une force. Nous pouvons la ressentir. C'est la force qu'il faut exercer pour soulever l'objet. De façon générale, nous expérimentons la matière en ressentant des forces. Les instruments scientifiques mesurent également des forces.
La masse est une notion abstraite qui en est dérivée par la réflexion, non par la perception. La distinction a été faite par Newton en étudiant la loi de la pesanteur (voir article Matière et rayonnements). Selon cette loi, le poids d'un objet est proportionnel à sa masse. Autrement dit, plus l'objet contient de matière, plus il est pesant. La masse de l'objet, c'est sa sensibilité au champ de gravité. Son unité est le kilogramme. Il est intéressant de remarquer que des sept unités qui forment le système international de mesures, l'unité de masse est la seule à être définie par un étalon matériel.
Par définition, la masse d'un corps est invariable où qu'il se trouve. Par contre le poids varie légèrement selon le lieu, en fonction de la force de gravité qui l'attire vers le sol. Cette force de gravité est moindre aux pôles qu'à l'équateur. Elle est beaucoup plus faible sur la lune, de sorte que les astronautes qui y ont marché se sont sentis plus légers même si leur masse n'avait pas changé.
Cette masse ainsi définie est appelée masse gravitationnelle, pour la distinguer d'un autre type de masse, la masse inertielle.
Nous expérimentons l'inertie comme une force assez curieuse. Si vous êtes debout dans un autobus en circulation, tout va bien tant que l'autobus avance à vitesse constante. Mais s'il freine, ou s'il accélère, ou s'il tourne, alors une force vous pousse contre la paroi. On la nomme la force d'inertie. Mais quelle est la cause de cette force, alors qu'aucun corps ni aucun rayonnement n'agit sur vous?
La physique ne sait pas répondre à cette question. Elle sait décrire cette force, la calculer, mais elle n'en connait pas la cause. La SED pourrait-elle suggérer une réponse?
Soit un objet immobile, par exemple une voiture en panne. Si nous devons la mettre en mouvement, il faut pousser d'autant plus fort que sa masse est grande. Elle résiste par sa masse d'inertie. L'inertie indique la résistance au changement de mouvement.
De même, si nous lançons une bille sur le sol, elle roule librement. Cela nous est familier de la voir poursuivre son mouvement à vitesse constante en ligne droite, jusqu'à ce qu'elle ralentisse et s'arrête. Partant de cette observation, on pensait jusqu'au 17e siècle qu'un corps détenait en lui une certaine impulsion intérieure, l'impetus (sorte de quantité de mouvement), qui s'épuisait peu à peu.
Puis on s'est aperçu que la bille ralentissait à cause des frottements du sol, mais que si on limitait ces petits accrochages, le mouvement pouvait durer plus longtemps. Le principe d'inertie stipule que un corps reste dans son état de mouvement sans changement tant qu'aucune action extérieure ne vient modifier ce mouvement.
Ce principe a été élaboré d'abord par Galilée (Dialogue sur les deux grands systèmes du monde, 1632), puis René Descartes (1596-1650) et Hans Christiaan Huygens (1629-1695). Descartes écrit (Principes philosophiques, 1644): Chaque chose, en tant qu’elle est simple et indivise, demeure, pour autant qu’il est en elle, toujours dans le même état, à moins que des causes extérieures ne la changent. Que tout mouvement est par lui-même droit; et ainsi, ce qui se meut en cercle, tendra toujours à s’éloigner du centre du cercle qu’il décrit.
C'est Isaac Newton (1642-1727) qui contribua à clarifier ce concept en énonçant sa première loi du mouvement des corps (Principia, 1687): Tout corps persévère dans son état de repos ou de mouvement rectiligne uniforme, à moins que des forces imprimées le contraignent d’en changer (voir article Matière et rayonnements). Cette loi est un principe, ce qui veut dire qu'on en donne l'énoncé, mais qu'on n'en connait pas la cause.
C'est ce principe qui permet de comprendre ce qui se passe pour vous dans l'autobus. Même si vous ne bougez pas, votre corps suit d'abord le mouvement de l'autobus qui avance à vitesse constante. Si le mouvement de l'autobus change, votre corps a tendance à vouloir conserver sa trajectoire par rapport au sol.
La notion de masse intervient dès qu'on veut modifier ce mouvement uniforme. Il faut appliquer une force pour accélérer ou freiner l'objet en mouvement. Il est plus facile de freiner un corps de petite masse qu'un corps de grande masse. Selon la deuxième loi de Newton, la force appliquée F est proportionnelle à l'accélération a. Le coefficient de proportionnalité est la masse inertielle (F=m.a). Changer la direction de mouvement est aussi une accélération, du point de vue de la mathématique de la mécanique.
En mesurant les masses inertielles et gravitationnelles, Newton a constaté qu'elles avaient la même valeur. Mais il ne comprenait pas pourquoi. C'est Albert Einstein qui eut la révélation que la force de gravitation était équivalente à une force d'accélération. En effet, dit-il, si vous vous trouvez dans un ascenseur que vous imaginez en chute libre, vous ne sentez plus votre poids, il est annulé. De plus tous les objets de l'ascenseur semblent immobiles par rapport à vous, comme si vous étiez dans un cadre immobile sans force de gravitation. Cela signifie que par l'accélération de la chute, le champ de gravitation est annulé dans l'ascenseur. Inversement, on peut créer une gravitation dans un habitacle si on le soumet à une accélération. Cette constatation conduira Einstein à élaborer sa théorie de la Relativité Générale.
Le concept de masse a reçu une autre interprétation dans le cadre de la physique des particules, basée sur la physique quantique relativiste.
La physique des particules est décrite par la théorie appelée modèle standard qui englobe la classification de toutes les particules sous-atomiques connues et la description de leurs interactions sous l'effet des forces électromagnétiques, nucléaires faibles et nucléaires fortes. Les interactions électromagnétiques et nucléaires faibles ont été réunies formellement en interaction électrofaible.
L'influence d'une onde électromagnétique sur une particule y est décrite comme l'échange de photons avec cette particule. De la même façon, toute interaction électrofaible (électromagnétique ou nucléaire faible) entre particules de masse est considérée comme un échange de particules virtuelles appelés bosons de jauge, incluant les photons.
Or le modèle standard, par le jeu des symétries, prévoit que toutes les particules seraient naturellement dépourvues de masse. Bien entendu, cela est contraire aux observations, et on sait bien que l'électron possède une masse (voir article Matière et rayonnement). Il a donc fallu modifier la théorie standard pour rendre compte de cette contradiction. Des physiciens - François Englert et Robert Brout d'une part, l'Écossais Peter W. Higgs d'autre part, ont proposé indépendamment en 1964 un mécanisme que la coutume a retenu sous le nom de mécanisme de Higgs.
Selon ce mécanisme, le vide n'est pas vide (tiens donc !). Il est plein d'un champ mathématique scalaire (ce qui signifie que sa valeur en chaque point est un nombre, au même titre qu'une carte des températures par exemple). Ce champ est nommé champ de Higgs. Une autre façon de le décrire est de le présenter comme un ensemble de bosons de jauge nommés bosons de Higgs ou BEH (Brout, Englert, Higgs). C'est un champ supplémentaire, qui se superpose aux champs correspondant aux interactions électrofaibles. Il a été proposé de façon abstraite, sans que personne n'en ait détecté l'existence.
Dans ce scénario, les particules virtuelles d'échanges qui interviennent dans l'interaction électrofaible (les bosons de jauge) acquièrent une masse en interagissant avec le champ de Higgs. Selon la formule du physicien français Étienne Klein, de la même façon qu'une personne qui se déplace dans une foule pour sortir d'une réception est freinée par ses nombreuses interactions de salutations aux autres personnes qu'elle croise, de la même façon, la masse de la particule est d'autant plus grande que son interaction avec les bosons de Higgs est forte. On a donc ces nouveaux bosons de Higgs qui donnent une masse aux bosons de jauge et aux autres particules.
Dans le site web de David Calvet, directeur de recherches au CNRS et membre du programme du LHC du CERN à Genève, on peut lire: Le 4 juillet 2012, le CERN a annoncé l'observation d'un boson de spin 0 qui semble correspondre au boson BEH attendu. Néanmoins, il faudra encore attendre quelques années pour avoir une réponse définitive à cette question: le nouveau boson est-il exactement celui qui a été prédit ?
Mais que veut dire au juste "observation"? Cela signifie-t-il qu'on l'a vu avec nos yeux? Absolument pas. C'est une interprétation, proposée dans le cadre de la théorie standard à l'exclusion de toute autre, d'un ensemble de signaux qui ont été détectés par le grand accélérateur de Genève, puis filtrés et traités. Et en effet, rien n'empêche que ces mesures reçoivent une autre interprétation dans un cadre formel différent. L'électrodynamique stochastique propose justement une autre interprétation de la masse.
Voici ce qu'en dit David Louapre dans son site science étonnante: Je ne sais pas pour vous, mais moi je n’aime pas trop cette façon de faire. Inventer une particule afin d’expliquer un phénomène expérimental qu’on ne comprend pas, pourquoi pas. Mais introduire artificiellement une nouvelle entité physique jamais observée, dans le seul but de sauver une théorie à laquelle on est attaché pour des raisons esthético-mathématiques, ça ne me paraît pas être une manière très correcte de faire de la science ! Si une théorie ne colle pas à la réalité, on la jette et on en change. On n’essaye pas de la sauver au prix de l’introduction de nouveaux objets physiques. Pour moi, c’est essayer de faire coller la réalité à la théorie, plutôt que l’inverse.
Enfin, il faut noter que même en admettant que le boson de Higgs existe bel et bien, et qu'il confère une masse à une particule, cela n'explique pas par quel mécanisme cette énergie que la particule lui prélève crée une résistance à son accélération. En contrepartie, si nous admettons l'existence d'un champ du point zéro, alors une explication se présente.
Pourquoi inventer un champ BEH pour justifier la notion de masse alors qu'il existe déjà un champ du vide, le champ du point zéro? C'est justement cette voie qu'ont suivie quelques chercheurs dans le cadre de la SED. Comme avec le champ BEH, la masse naitrait de la résistance que le vide oppose à la particule. Des charges électriques sans masse plongées dans les champs électromagnétiques créent l'apparence de masse.
Lorsqu'une particule chargée est placée dans le vide, elle est soumise à l'influence des ondes électromagnétiques du champ du point zéro, comme nous l'avons signalé plusieurs fois. Si elle est animé d'un mouvement uniforme, on peut simplement noter que sa trajectoire fluctue à cause des fluctuations du vide.
Si la particule est accélérée linéairement ou déviée, alors il se passe quelque chose de nouveau dans le vide. Du point de vue de la particule, les ondes du vide changent en composition. Cela crée une force qui tend à s'opposer au mouvement. C'est cette force qui apparait comme le phénomène d'inertie. L'inertie ne serait donc pas intrinsèque à la matière, mais due à une influence extérieure.
Ce raisonnement est valide aussi bien dans le cadre du champ du point zéro de l'électrodynamique quantique que dans celui de l'électrodynamique stochastique.
Il a été développé dès les années 1990 plus particulièrement par Harold (Hal) Puthoff (né en 1936), directeur de l'Institute for Advanced Studies à Austin au Texas et d'une société de recherche EarthTech International, par l'astrophysicien Bernhard Haisch du laboratoire de recherches de Lockheed à Palo Alto et par Alfonso Rueda au California State University à Long Beach, tous aux États-Unis.
 |  |
| Harold Puthoff Merci à Biblioteca Pleyades | Bernhard Haisch Merci à SuperConsciousness |
Ils ont calculé que la force de résistance qui apparait dans la molécule est proportionnelle à l'accélération de la particule. C'est conforme à la seconde loi de Newton.
Considérons une particule chargée de volume V0. Elle baigne dans le champ du point zéro. Lorsqu'elle est animée d'un mouvement accéléré, il la traverse partiellement et interagit avec elle avec un certain coefficient d'opacité η qui dépend du mécanisme d'interaction.
On calcule la quantité de mouvement p du flux de ce champ à travers la particule, puis la force exercée dp/dt. On trouve que cette force est proportionnelle à l'accélération a: F=mi.a
Le coefficient de proportionnalité mi est la masse inertielle. Elle est fonction de h et de c:
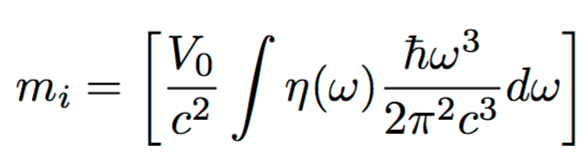
Le raisonnement de Haisch et Rueda est le suivant. La particule chargée a un volume V0. Le champ imprègne tout l'espace, y compris l'intérieur de la particule. Lorsqu'elle se déplace, les radiations passent à travers elle. Tant que son mouvement est uniforme, elles restent identiques. Mais si le mouvement est accéléré, ces radiations sont diffusées avec une densité différente. Ce changement de densité crée une résistance.
D'où leur définition de la masse: La masse inertielle d'un objet est la fraction de l'énergie de radiation du champ du point zéro incluse dans l'objet qui interagit avec lui.
On sait, depuis qu'Einstein a élaboré sa théorie de la Relativité Restreinte, que la masse est équivalente à une quantité d'énergie selon sa célèbre formule E=mc2, où c est la vitesse de la lumière dans le vide.
La formule est une chose, son interprétation en est une autre. Que signifie-t-elle vraiment?
Les physiciens y voit une énergie qui est stockée sous forme de masse. Il est donc possible de transformer cette masse en énergie pure. Par exemple, dans une réaction de désintégration nucléaire, lorsqu'un atome se scinde en deux autres atomes, la somme des masses des atomes produits n'est pas égale à la masse de l'atome d'origine. La différence est égale à l'énergie qui a été libérée sous forme de chaleur et de rayonnements.
Inversement, l'énergie peut se matérialiser en particule. C'est pourquoi, dans le cadre de la théorie quantique des champs, le champ d'énergie du point zéro qui est pure énergie électromagnétique peut donner naissance à des paires d'électron+positron.
Or dans le cadre de la SED, la masse EST de l'énergie. Elle n'est pas seulement convertible en énergie, elle est déjà énergie, sous la forme d'énergie du CPZ condensée dans un petit volume. La formule d'Einstein donne la quantité d'énergie amassée qui confère à la particule l'illusion d'une certaine masse. C'est donc une toute autre vision de l'univers et de la matière.
Étant donné que la masse gravitationnelle et la masse inertielle sont identiques, il doit également être possible de trouver l'origine de la force de gravitation dans le champ du point zéro. C'est le raisonnement qu'ont développé les chercheurs déjà nommés (Puthoff, Haisch, Rueda...) dans le cadre de la SED.
Selon Haisch et Rueda (2005), lorsque vous placez un gros objet dans l'espace, sa présence distord le champ. Si vous vous placez à un endroit proche de cet objet, le champ du vide est accéléré à travers vous, et cela crée la force de gravitation. Ils ont montré que la situation de la force de gravitation est la même que celle de la force d'inertie. Il suffit pour décrire la particule de passer d'un repère mathématique fixe où elle subit la gravité, à un repère accéléré où elle ne la ressent plus. C'est le même système vu de deux façons différentes. Les deux masses sont les mêmes, car il s'agit du même processus.
Affirmer que la force de gravitation prend son origine dans les interactions avec le champ du point zéro est révolutionnaire puisque cela modifie les bases du modèle standard. D'après celui-ci, la gravitation fait partie des 4 forces fondamentales qui fondent et régissent l'univers et la matière (électromagnétique, nucléaires faible et forte, gravitation).
Toutefois, même dans le modèle standard, la force de gravitation tient un rôle à part parmi les quatre forces. Des théories sophistiquées ont permis d'unifier les forces électromagnétiques et nucléaires faibles, en leur trouvant une origine commune à très haute température. De même on a pu unifier cette force électrofaible avec la force nucléaire forte. Mais la gravitation résiste aux efforts d'unification mathématique, à moins de faire appel à des théories extrêmement compliquées et peut-être artificielles, les théories des cordes.
De plus dans ce modèle, on ne comprend pas la nature de cette force d'attraction, et par quel moyen une masse peut la créer.
On sait seulement énoncer la loi qui donne la valeur de la force d'attraction que deux masses m1 et m2 exercent entre elles: F=G m1.m2/d2, avec G, constante universelle de gravitation.
Cette ignorance provient peut-être tout simplement du fait que la gravitation ne constitue pas une force fondamentale. Selon la SED, elle est dérivée de la force électromagnétique.
L'idée n'est pas nouvelle. C'est ce qu'a proposé en 1967 le physicien russe Andreï Sakharov (1921 - 1989), connu aussi comme courageux militant pour les droits de l'Homme dans l'URSS dictatoriale de cette époque, et prix Nobel de la paix en 1975.
Sakharov cherchait un ensemble d'hypothèses fondamentales minimales, desquelles seraient déduites les équations de la Relativité Générale. Pour lui, la force de gravitation proviendrait des fluctuations du champ du point zéro, modifiées par la présence de la matière. Si on place deux particules proches, pensait-il, la première fait écran à une partie des influences du champ du point zéro. Il en est de même réciproquement de la deuxième particule sur la première. C'est une variante du système de Casimir, où les plaques sont remplacées par des particules.
Dans un premier temps, aux alentours de 1990, Puthoff avait traduit cette idée sous forme mathématique. Il a développé un modèle où les particules étaient traitées comme des oscillateurs qui modifient le champ. Plongées dans le champ, leurs positions fluctuent (elles tremblent). Une force d'attraction apparait entre les deux particules de la même façon que les forces de Van der Waals, mais sur une échelle beaucoup plus grande. Toutefois, cette voie ne permettait pas de rendre compte mathématiquement de la formule de la force. Il est possible que ces calculs reposent sur des bases trop simplifiées.
Mais cela a montré que la constante de gravitation universelle G pouvait être appréhendée par ce moyen. Elle pouvait être exprimée en fonction de la vitesse de la lumière et de la constante de Planck. Par la suite, Puthoff a un autre modèle basé sur la polarisation du vide.
Si l'espace est constitué d'énergie, en quantité quasiment infinie, serait-il possible d'en extraire afin de nous approvisionner? La question a été posée, et des systèmes théoriques ont été proposés.
Un système qui tire parti du phénomène de Casimir a été imaginé par Robert Forward en 1984. Si on laisse les plaques s'attirer, elles se cognent et produisent de la chaleur qu'on peut récupérer. Mais cela fait, le phénomène s'arrête. Il faut dépenser l'énergie recueillie pour séparer les plaques à nouveau. Il faut donc en utiliser de nouvelles si on ne veut pas faire cette dépense d'énergie.
Le principe a été repensé par Puthoff. Il propose qu'on utilise un système avec beaucoup de plaques "jetables". Ces "plaques" seraient des ions, donc sous forme d'un gaz ionisé, un plasma. On effectue d'abord une forte contraction du plasma pour dépasser la barrière de répulsion électrique, et la force de Casimir condenserait ensuite les molécules. On pourrait recueillir l'énergie produite.
Une autre façon de modifier le champ en changeant la répartition des fréquences a été imaginée dans un brevet en 1996 par Mead et Nachamkin. Ils proposent l'emploi de sphères diélectriques résonnantes légèrement désaccordées pour créer des battements et décaler certaines hautes fréquences.
Pour le moment, il ne s'agit que de spéculations et de calculs qui montrent que c'est en principe possible. Des laboratoires se sont penchés sur leur réalisation pratique, mais à ma connaissance, aucune n'a abouti.
Dans des articles futurs, nous explorerons d'autres voies de réalisation technique, issues de théories différentes qui ont été plus fructueuses.
Accéder aux autres parties:
Un livre qui fait le point sur la question: Luis de la Peña, Ana Maria Cetto, Andrea Valdes-Hernandez, 2014, The Emerging Quantum: The Physics Behind Quantum Mechanics, Springer International Publishing AG
De Trevor W. Marshall:
T.W. Marshall, Random Electrodynamics, 1963, Proc. Roy. Soc. A, 275, 475-491. La publication fondatrice de la SED
T.W. Marshall and Emilio Santos, 1997, The
myth of the photon, The Present Status of the Quantum Theory of Light, ed. S. Jeffers et al., Kluwer, Dordrecht, 1997, pages 67 - 77
T.W. Marshall, 1997, The
myth of the down converted photon, Cornell University Library, Quantum physics archives
T.W. Marshall, 1997, The
zeropoint field — no longer a ghost, Cornell University Library, Quantum physics archives
T.W. Marshall, 2002, Nonlocality
- The party may be over, Cornell University Library, Quantum physics archives
T.W. Marshall, 2011, Can
we celebrate Defeat for the Photon by Maxwell-Planck theory?, site web Crisis in physics
De Timothy H. Boyer:
T.H. Boyer, 1973, Retarded
van der Waals forces at all distances derived from classical electrodynamics with classical electromagnetic zero-point radiation, Phys. Rev. A, Vol. 7, 6, 1832-40
T.H. Boyer, 1975, Random
electrodynamics: The theory of classical electrodynamics with classical electromagnetic zero-point radiation, Phys. Rev. D 11, 790
T.H. Boyer, 2010, Blackbody radiation and the scaling symmetry of relativistic classical electron theory with classical electromagnetic zero-point radiation, Found. Phys. 40, 1102-116
T.H. Boyer, 2011, Any Classical Description of Nature Requires Classical Electromagnetic Zero-Point Radiation, Cornell University Library, Quantum physics archives (disponible également dans ce site)
T.H. Boyer, 2012, Is Planck’s Constant h a “Quantum” Constant? An Alternative Classical Interpretation, Cornell University Library, Quantum physics archives (disponible également dans
ce site)
Harold E. Puthoff, 1988, Zero-point
fluctuations of the vacuum as the source of atomic stability and the gravitational interaction, Proceedings of the British Society for the Philosophy of Science, International Conference "Physical Interpretations of Relativity Theory", London
Daniel C. Cole and Yi Zou, 2003, Quantum
mechanical ground state of hydrogen obtained from classical electrodynamics, Phys. lett. A 317 14-20
L. de la Peña, A. M. Cetto, 2005, Contribution
from stochastic electrodynamics to the understanding of quantum mechanics, Cornell University Library, Quantum physics archives
Emilio Santos, 2014, Stochastic electrodynamics and the interpretation of quantum physics, Cornell University Library, Quantum physics archives
Optique du cristal:
Sun Jinyu, Zhang Shian, Jia Tianqing, Wang Zugeng, Sun Zhenrong, 2009, Femtosecond
spontaneous parametric upconversion and downconversion in a quadratic nonlinear medium, Journal of the Optical Society of America B 26, 3, 549
S. Akbar Ali, P. B. Bisht, A. Nautiyal, V. Shukla, K. S. Bindra, and S. M. Oak, 2010, Conical
emission in β-barium borate under femtosecond pumping with phase matching angles away from second harmonic generation, Journal of the Optical Society of America B 27, 9, 1751
Vitesse de la lumière:
Helen D. Setterfield, Upheaval in Physics: History of the Light-Speed Debate
Barry Setterfield, 1981, The
Velocity of light and the age of the universe, Creation 4, 1, 38
Barry Setterfield & Trevor Norman, 1987, The
Atomic Constants, Light, and Time, prepared for Lambert T. Dolphin
V. S. Troitskii, 1987, Physical Constants and the evolution of the Universe, Astrophysics and Space Science, 139, 389
Implications of Non-Constant Light Velocity, collected by Lambert Dolphin
Masse et gravitation:
Harold E. Puthoff, 1989, Gravity
as a zero-point-fluctuation force, Phys. Rev. A 39, 2333
H.E. Puthoff, 1990, Everything
for Nothing, New Sci. 127, 52
H. E. Puthoff, 1991, Zero-Point
Energy: An Introduction, Fusion Facts 3, 3, 1
D. C. Cole, H. E. Puthoff, 1993, Extracting
Energy and Heat from the Vacuum, Phys. Rev. E 48, 1562
Bernhard Haisch, Alfonso Rueda & H.E. Puthoff, 1994, Inertia
as a zero-point-field Lorentz force, Phys. Rev. A, 49, 2, 678
B. Haisch, A. Rueda & H.E. Puthoff, 1997, Physics
of the zero-point-field: Implications for inertia, gravitation and mass, Speculations in Science & Technology, 20, 99
A. Rueda & B. Haisch, 1998, Contribution
to inertial mass by reaction of the vacuum to accelerated motion, Found. Physics, 28, 7, 1057; Inertial
mass as reaction of the vacuum to acccelerated motion, Physics Letters A, 240, 3, 115
Daniel C. Cole, Alfonso Rueda, Konn Danley, 2001, Stochastic
nonrelativistic approach to gravity as originating from vacuum zero-point field van der Waals forces, Physical Review A, 63, 054101
Paul S. Wesson, Zero-point fields, gravitation and new physics, rapport pour le California Institute for Physics and Astrophysics
A. Rueda & B. Haisch, 2005, Gravity
and the quantum vacuum inertia hypothesis, Annalen der Physik, 14, 8, 479
E. W. Davis, V. L. Teofilo, B. Haisch, H. E. Puthoff, L. J. Nickisch, A. Rueda and D. C. Cole, 2006, Review
of Experimental Concepts for Studying the Quantum Vacuum Field, Space Technology and Applications International Forum, 1390
Énergie
Robert Forward, 1984, Extracting electrical energy from the vacuum by cohesion of charged foliated conductors, Phys. Rev. B, 30, 1700
H.E. Puthoff, 1990, The
energetic vacuum: implications for energy research; speculations in science and technology, 13, 4, 247
| |
Texte conforme à la nouvelle orthographe française (1990)
2 juin 2016