

Des particules aux galaxies,
 La Spirale
La Spirale
mouvement primordial de vie
Alain Boudet
Dr en Sciences Physiques
Résumé: Les spirales sont présentes à tous les niveaux de la création, depuis les molécules jusqu'aux galaxies. La spirale est un mouvement fondamental inscrit dans la structure de l'univers. Elle se manifeste sous différentes formes (plane, conique ou cylindrique) dans les plantes, les animaux et l'être humain. Dans l'air, l'eau et le sang, elle est le mouvement naturel de vie. On peut redynamiser l'eau et les rivières par des systèmes concrets en spirale. De nouveaux moteurs puissants, économiques et non polluants existent sur ce principe.
De tout temps, les peuples anciens ont représenté et vénéré la spirale comme la source créatrice qui nous nourrit et qui se développe en nous, mais dont nous sommes éloignés. Sous la forme du dieu serpent Quetzalcoatl, elle est la force salvatrice qui rétablit la connexion d'origine. Lorsque nous marchons sur un trajet en spirale labyrinthique, nous redressons notre état énergétique et nous retrouvons l'intégrité de notre âme.
SPIRALE ! Que vous évoque ce mot?
Vous connaissez les cahiers à reliure spiralée et les galaxies en spirale.
Et le mot hélice? À votre avis, a-t-il un rapport avec la spirale? Lequel?
Vous connaissez probablement l'hélice du bateau et l'hélice de l'ADN qui sont désignées par le même mot, mais qu'ont-elles en commun?
Les mots Spirales et Hélices nous renvoient à de nombreux domaines, aussi bien dans notre quotidien que dans les fondements de la matière. Ils peuvent nous évoquer de belles images et des émotions esthétiques. Mais beaucoup parmi nous ne sauraient pas préciser ce qu'ils désignent. Voici donc un article introductif qui a pour but de vous familiariser avec ces notions et de vous entrainer dans le monde fabuleux des spirales.
Car les spirales et les hélices sont à la base du mouvement et de la vie.
Nous commencerons par dénicher des spirales et des hélices dans notre monde environnant. Nous allons constater qu'elles sont nombreuses et se présentent sous des apparences variées. Puis nous allons explorer l'infiniment grand et l'infiniment petit et nous constaterons que la spirale se manifeste à toutes les échelles. Nous découvrirons alors que bien plus qu'une forme, la spirale est une force fondamentale inscrite dans la structure de l'univers.




La spirale se décline sous de nombreuses variantes qu'on peut classer en 3 formes principales que nous allons examiner successivement: les spirales planes, les spirales coniques et les vortex, les spirales cylindriques ou hélices. On peut y ajouter la forme serpentine ou ondulée (méandres) qui est dérivée de l'hélice.

Nous faisons facilement l'expérience de la spirale plane en manipulant des objets de notre quotidien, un tuyau d'arrosage par exemple. Je prends un tuyau d'arrosage et je veux l'enrouler sur le sol plat. Je pose d'abord une extrémité du tuyau, et je dessine un premier tour d'enroulement autour de cette extrémité en suivant une forme proche d'un cercle. Le second tour vient s'enrouler autour du premier en s'éloignant du centre. Et ainsi de suite.
Je viens de créer une spirale plane. Chacun des tours est appelé une spire.
Plus je continue à enrouler le tuyau, plus je m'éloigne du centre et plus grande est la longueur du tuyau nécessaire pour faire une nouvelle spire. Sur la photo de mon tuyau, j'ai 13 spires. Si je prolonge mon tuyau par un autre, j'aurai un nombre de spires bien plus grand. Une spirale peut toujours être prolongée et en théorie elle peut comporter un nombre infini de spires.
Pour faire connaissance de façon concrète avec les spirales planes, observons celles qui sont présentes dans les objets qui nous entourent. Des spirales planes se forment naturellement lorsqu'on enroule les tuyaux, boudins, tubes et fils, autrement dit des objets longs et souples. On trouve aussi des spirales dans des objets en dur fabriqués par l'être humain.
 |  | ||
| Rouleau de merguez sur un étal © A. Boudet | Cordage Merci à Stonk Knots | Hélicons Merci à Wikimédia | Manche d'une contrebasse Merci à Wikimédia |
Dans ses manifestations, la spirale apparait parfois par fonctionnalité ou commodité. L'hélicon enroulé est plus facile à manier qu'une longue trompe allongée. La saucisse enroulée sur un présentoir prend moins de place. Mais en plus, sa forme harmonieuse attire l’œil. La spirale est souvent choisie pour son esthétique. Enfin, elle est aussi chargée de symbolisme, en évoquant la force de vie et de déploiement (voir plus loin). Ces quelques exemples nous font déjà entrevoir l'abondance des spirales.
Les 4 exemples présentés ci-dessus montrent des spirales dont les spires sont bien tassées les unes contre les autres. On obtient d'autres formes de spirales en modifiant l'écartement des spires. Ainsi, les spires du tuyau présenté plus haut sont écartées de façon plus lâche et moins régulière que les 4 exemples précédents.
Pour illustrer cette variété, je vais m'aider de graphismes. Mais plutôt que de prendre des dessins tracés sur papier ou sur ordinateur, je vous propose des dessins de spirales qui ont été imprimées dans des champs. De magnifiques diagrammes (crop circles ou cercles de culture) de plusieurs dizaines de mètres de diamètre sont découverts chaque été dans les cultures situées pour la plupart dans le sud-ouest de l'Angleterre. Ce phénomène fantastique se produit depuis une trentaine d'années et nous régale de graphismes géométriques d'une variété, d'une beauté et d'une précision mathématique extraordinaires. On y trouve des spirales aussi bien que des cercles, rosaces, triangles, étoiles, et toutes leurs combinaisons, ainsi que des pictogrammes (voir article Diagrammes dans les champs pour plus d'informations et pour découvrir d'autres photos).
 |  |
| Cercle de culture, Bracciano, Italie. Signalé le 20 Mai 2012 Merci à Crop circle connector | Cercle de culture, Pewsey, Angleterre Signalé le 17 juillet 2002 Merci à Temporary Temples © |
Dans ces diagrammes de champs, voici 2 exemples de spirales planes. À gauche, les spires sont un peu écartées. Toutefois leur écartement reste constant d'une spire à l'autre. Si par contre l'écartement est de plus en plus grand d'une spire à la suivante, on obtient une spirale de type escargot comme sur la figure de droite.
Lorsque la spirale a une forme bien régulière, on peut la décrire par une formule mathématique qui donne la valeur de l'écartement selon l'endroit désigné sur la spirale. En fonction de cette formule, on peut distinguer différents types de spirales planes: logarithmique, hyperbolique, d'Archimède, de Fermat, de Fibonacci, le lituus, etc. (voir annexe pour plus de précisions).
Je prends maintenant une corde, qui est plus souple que le tuyau, et je la replie en deux brins. Puis j'enroule le double brin en spirale à partir du centre. Nous avons donc maintenant deux branches qui se déploient à partir du centre. C'est une spirale à deux bras.
 |  |  |
| Spirale à 2 bras Cercle de culture, West Overton, Angleterre Signalé le 23 juin 2002 Merci à Temporary Temple © | Spirale à 3 bras Cercle de culture, Windmill Hill, Angleterre Signalé le 29 juillet 1996 Merci à Temporary Temple © | Spirale à 6 bras Cercle de culture, Milk Hill, Angleterre Signalé le 14 aout 2001 Merci à Lucy Pringle © |
Sur le même principe, à partir du cœur de la spirale, on peut faire sortir plusieurs bras (branches), pour former des spirales à 3 bras, 4 bras, ou même beaucoup plus. Les images de crop circles nous en offrent quelques exemples (d'autres se trouvent dans l'article Diagrammes de champs)
Imaginons une spirale plane faite en fil de fer assez rigide, du type d'un ressort, ou en guirlande plastique lumineuse (comme sur l'illustration). Nous en soulevons doucement l'extrémité centrale. Grâce à sa rigidité, le fil ou le tube conserve sa forme enroulée, tout en se déployant verticalement, comme s'il était dessiné sur une surface conique.
Nous obtenons une spirale conique. Il existe donc une continuité entre la spirale plane et la spirale conique par le soulèvement (ou affaissement) du centre en-dehors du plan de base.
 |  |  | |
| Arbre lumineux | Spirale conique inclinée D'après Mathcurve | Cercle de culture, Windmill Hill, Angleterre Signalé le 30 juin 2006 Merci à Temporary Temple © | Même photo retournée. L'impression de relief est différente. |
Si nous soulevons l'extrémité centrale en travers, et non verticalement, on obtient une spirale conique inclinée.
Comme la spirale plane dont elle dérive, la spirale conique nous amène d'un centre vers l'extérieur (à moins qu'on la parcourt dans l'autre sens). Mais le centre est maintenant marqué par une pointe, un sommet.
Le terme vortex est employé pour désigner le mouvement spiralé d'un fluide liquide ou gazeux, ou même un mouvement de particules et d'ondes. Dans le langage populaire, une spirale conique qui se manifeste dans un liquide en mouvement est un tourbillon.
Si la spirale conique se manifeste dans un objet déformable qu'on tord, c'est une torsade ou tortillon.
 |  | 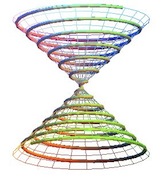 |
| Tortillon d'une épluchure de pomme Merci à Plus.be | Tortillon, un gâteau sec de la ville de Bon-Encontre Merci à Boulangerie Artisanale | Spirale sur un double cône Merci à © Robert Ferréol |
Si le cône se prolonge au-delà de sa pointe en double cône, la spirale qui se dessine à sa surface comporte deux parties symétriques. On peut commencer le voyage sur cette spirale en entrant par l'une des bases, puis on se rapproche du centre, on le traverse et on repart vers l'extérieur par l'autre base.
Les spirales planes peuvent se distinguer par le sens de leur rotation. Comment le définit-on? Revenons au tuyau que j'enroule. En partant du centre pour le premier tour, j'ai la liberté de l'enrouler vers la droite (comme sur la photo vue plus haut) ou vers la gauche. J'obtiens donc deux sortes de spirales, les spirales droites et les spirales gauches.
 |  | 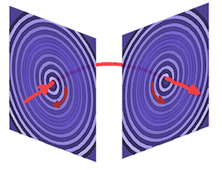 |
| Spirale dextrogyre (qui tourne à droite) | Spirale lévogyre (qui tourne à gauche) | Le spirale droite devient gauche si on la regarde dans l'espace par l'autre côté |
Toutefois, si j'ai un tuyau enroulé en spirale droite par exemple, j'ai la liberté de le soulever puis de le retourner et je vois alors une spirale gauche. Faites l'expérience avec une feuille de papier sur laquelle vous dessinez une spirale droite. Retournez la feuille et vous voyez une spirale gauche. Et c'est bien toujours le même objet disposé différemment. Dans l'espace, le sens de la spirale plane dépend de la face par laquelle nous la regardons, si nous nous plaçons par dessous ou par dessus par exemple. Ce sens n'est donc pas défini intrinsèquement pour l'objet lui-même.
Il n'est véritablement possible de distinguer les deux sens que si les spirales planes sont astreintes à rester posées, gravées, ou dessinées sur une surface fixe, comme sur cet écran, sur une feuille fixée au mur, sur le sol ou sur un rocher. Ce n'est pas la cas des galaxies, par exemple, qu'on pourra regarder dans un sens ou l'autre quand on se baladera dans l'espace (voir plus loin Spirales galactiques). Idem pour un ouragan dont le sens apparait différent selon qu'on le regarde du sol ou d'un satellite.
Même chose pour les spirales coniques, le sens perçu s'inverse selon que je regarde au-dessus de la pointe (en relief) ou par dessous (le creux du cône). Toutefois, cette fois, les deux faces ne sont pas équivalentes et il ne revient pas au même de tourner sur le relief ou dans le creux. En effet, si je regarde une spirale conique donnée par-dessus la pointe, et si je suis la spirale avec mon doigt à partir de son sommet (disons qu'elle tourne à droite), mon doigt s'éloigne de moi. En tournant, il avance. Si je regarde la même spirale par le dessous creux, mon doigt tourne à gauche à partir de la pointe en se rapprochant de moi, il recule.
La symétrie qui existait dans la spirale plane est rompue par la pointe qui sort du plan de base. On retrouve bien les deux sens de rotation selon le côté regardé, mais ils s'accompagnent d'un mouvement différent. Comme il est préférable d'avancer plutôt que de reculer, on a décidé de nommer le sens de la spirale conique par le type de rotation qu'on effectue en avançant sur la spirale. Dès lors, pour les spirales coniques on peut parfaitement distinguer les spirales qui tournent à droite (comme notre épluchure de pomme ci-dessus) et celles qui tournent à gauche (comme le tortillon).
Lorsque la spirale est enroulée sur la surface d'un cylindre, par exemple un bâton, on obtient un autre type de spirale, la spirale cylindrique ou spirale circulaire, ou encore hélice. L'hélice est très courante dans notre quotidien. Par exemple, c'est une autre façon d'enrouler les tuyaux ou autres tubes souples et cordages.
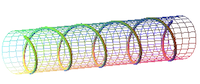 |  |  |
| Hélice circulaire ou cylindrique Merci à Robert Ferréol | | Reliures spiralées Merci à Wikimédia |
Avec l'escalier en colimaçon, nous faisons physiquement l'expérience de l'hélice. Lorsqu'on le gravit, chaque fois qu'on arrive à l'étage supérieur, on a effectué un tour d'hélice, on arrive au-dessus du point de départ au sol. Après chaque tour d'hélice, on s'élève de la même hauteur, la hauteur d'un étage. Cela caractérise une hélice régulière. Cette distance entre deux niveaux d'une hélice régulière est appelée son pas.
En tournant, on s'élève, on progresse. La rotation sur l'hélice produit une progression, un avancement, contrairement au cercle où on se retrouve au même point après un tour.
 |  |  | 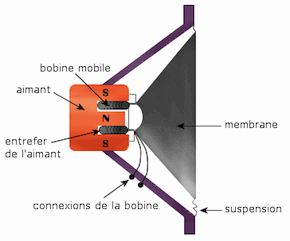 |
| Escalier hélicoïdal | Boulon | Tire-bouchon | Principe d'un haut-parleur |
On trouve des hélices régulières dans le tire-bouchon, dans le filetage des vis, des boulons et des écrous. Dans les deux cas, la rotation s'accompagne d'un avancement: le tire-bouchon s'enfonce dans le bouchon et le boulon s'enfonce dans l'écrou.
Lorsqu'un courant électrique parcourt un fil de cuivre enroulé en hélice, il crée un champ magnétique intense à l'intérieur de la bobine. Ce dispositif nommé solénoïde est très utilisé en électricité, par exemple dans les électroaimants. Ces bobines sont également des parties essentielles des haut-parleurs et des moteurs électriques.
La spirale hélicoïdale dérive de la spirale conique par une déformation continue. Imaginons que le cône est en une matière élastique telle qu'une genouillère. On passe la main ou un gros bâton dans le creux pour écarter le sommet jusqu'à ce que son diamètre soit aussi large que la base. On a alors un cylindre.
On peut aussi dessiner une ligne droite oblique sur une feuille de papier que l'on enroule. Si on l'enroule en cône, on a la spirale conique. Si on l'enroule en rouleau, on obtient une hélice.
Comme dans le cas de la spirale conique, on distingue des hélices droites et des hélices gauches. En suivant la convention indiquée plus haut qui définit le sens d'une hélice, le boulon est une hélice droite car c'est en tournant le boulon vers la droite qu'il avance. Il existe des cas spéciaux de boulons à gauche pour raison de sécurité dans des axes de moteurs. Le tire-bouchon est également doté d'une hélice droite, sauf ceux des farces et attrapes qui sont à gauche.
Sur un cylindre, on peut dessiner plusieurs hélices de même pas, mais décalées. Selon le même principe que les spirales planes à plusieurs bras, on obtient des hélices à multiples bras ou brins. Les hélices de propulsion de bateaux ou d'avions et les éoliennes sont conçues de cette façon (voir en annexe). La molécule d'ADN est faite de 2 brins enroulés en hélice (voir plus loin).
Nous sommes partis de la spirale dessinée sur une surface plane. Elle s'est développée en volume avec la spirale conique et l'hélice. Si maintenant nous aplatissons l'hélice par le côté, nous trouvons la sinuosité (courbe sinusoïdale). En effet, regardons à nouveau le tire-bouchon ci-dessus en silhouette, donc en enlevant la profondeur de vue. Cela revient à projeter l'ombre de l'hélice sur une surface. Nous voyons un S. De profil, l'hélice ondule en méandres ou prend l'allure d'un serpent.
 |  |  |  |
| L'hélice, vue à plat, parait une suite de méandres | Serpent, instrument de musique médiéval Merci à Wikimedia | Cercle de culture, Barbury Castle, Angleterre Signalé le 5 aout 1999 © Temporary Temples | Cercle de culture, East Field,, Angleterre Signalé le 17 juin 1996 Merci à Temporary Temples © |
De même que la spirale plane, le vortex ou l'hélice, les méandres nous évoquent la force de vie. Ici, il s'agit de force d'avancement, de transport, de progression. Les serpents avancent en ondulant. Les signaux de télécommunication sont transportés par des ondes électromagnétiques sinusoïdales.
Force de vie, la spirale est naturellement présente dans la nature avec une grande variété de formes, y compris la sinuosité. On la rencontre abondamment parmi les plantes, les animaux, les paysages, et dans le corps humain.
Chez les animaux, les ondulations sont manifestes chez les serpents. Ceux-ci adoptent d'ailleurs volontiers la forme spiralée pour dormir.
On trouve la spirale dans les cornes de certains bovins ou caprins et dans le dessin des coquilles de certains coquillages.
 |  |  |
| Serpent à collier Merci à Aquajardin | Un orvet se replie en spirale Merci à Petit monde du pote agé | Bélier Merci à Golden Mudeum |
Les spirales des coquillages sont pour la plupart coniques. Observons un escargot. Avez-vous remarqué que sa moitié gauche est différente de la droite? L'une part en pointe (nommée aussi apex). Ce qui est étonnant, c'est que la pointe est presque toujours située à droite par rapport à l'avant de l'escargot, rarement à gauche. On voit donc la spirale tourner à droite. Vérifiez-le.
On trouve aussi la forme spiralée conique dans le squelette siliceux des radiolaires, petits animaux dont la taille varie de 1 mm à 1 cm.
 |  |  | 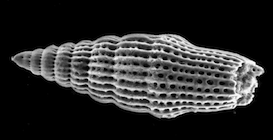 |  |
| Escargot de bourgogne Merci à Education - Environnement | Escargot Merci à Maths pour les nuls | Coquillage marin | Radiolaire Merci à Museum of Paleontology | Ammonite et nautile |
Quelques coquillages ont des coquilles symétriques. Ils sont donc plans, à la façon d'un tuyau enroulé qui va en s'évasant. C'est le cas des argonautes, ainsi que des nautiles qui sont des sortes de pieuvre. À l'intérieur de la coquille, l'animal est entouré d'un tissu (le manteau) qui secrète les constituants de la coquille. Au fur et à mesure que l'animal grossit, la coquille s'allonge, prend du volume et s'épaissit.
Les ammonites, qui sont des coquillages fossiles, ont aussi une coquille plane. On en trouve facilement dans certains terrains de sédiments. Le fossile est constitué de terre, qui s'est logée dans la forme interne de la coquille d'origine et en a moulé la forme. La coquille n'est généralement pas conservée. Les ammonites peuvent atteindre jusqu'à 2 m de diamètre.
Parmi les plantes, mentionnons les crosses de la fougère arborescente et les jeunes pousses de petits pois qui ont une forme de spirale plane. Même dans une photo qui les représentent figées, on les sent prêtes à se dérouler. Dans l'aloe polyphylla, la spirale, extrêmement marquée, comporte 4 branches régulières.
La spirale nous suggère le mouvement de déploiement, associé à la croissance et à l'évolution de la plante. Il en est de même dans les coquillages.
 |  |  |  |
| Pousse de petit pois Merci à Robert Ferréol | Aloe polyphylla Spirale droite à 4 branches Merci à Etsy | Fleur de tournesol 34 spirales droites, 21 spirales gauches Merci à Anthropologie | Pomme de pin 13 spirales droites, 8 spirales gauches |
Ce qu'on désigne ordinairement par la fleur de tournesol est en réalité composé d'une multitude de petites fleurs appelées fleurons, qui deviendront les graines. Par leurs emplacements, ces fleurons dessinent des spirales. Chacun d'entre eux est situé à l'intersection d'une spirale qui tourne à droite et d'une autre qui tourne à gauche. La fleur est donc structurée par plusieurs spirales gauches et droites. Il en est de même pour la pomme de pin dont les spirales sont dessinées par l'emplacement des écailles. L'existence de spirales donne l'impression de mouvements, mais le fait qu'elle soient dans les deux sens leur confère un aspect globalement plus statique.
Dans la fleur de tournesol représentée ici, on dénombre 21 spirales gauches et 34 droites. Dans la pomme de pin, 8 et 13. Ces nombres sont remarquables, car ils appartiennent à la série de nombres appelée série de Fibonacci. Ces nombres résultent de la valeur de l'angle entre deux fleurons ou écailles successifs au cours de la croissance. C'est l'angle d'or, qui est de 137,5° (voir explications en annexe).
On trouve aussi cette disposition dans les tiges de nombreuses plantes. Lorsque les feuilles ou les épines apparaissent sur la tige, elles ne sont pas disposées au hasard. Elles peuvent apparaitre 2 par 2, et se font face. Ou alors, elles sont isolées et sont disposées en hélice.
La spirale est un schéma constitutif de nombreuses formes de vie et de structures de la matière, non seulement dans les plantes et les animaux, mais à toutes les échelles de réalité, depuis l'infiniment grand cosmique à l'infiniment petit atomique.
Allons la rencontrer dans l'infiniment grand en nous élevant dans le cosmos. Nous la trouvons inscrite dans de nombreuses galaxies.
Une galaxie est formée d'une multitude d'étoiles distribuées de façon non-homogène. Les régions où elles sont regroupées en plus grande densité nous apparaissent plus brillantes. Quand je dis "nous apparaissent", cela signifie apparaissent à travers différents instruments optiques, tels que télescopes et spectrographes, qui recueillent les signaux électromagnétiques envoyés par ces étoiles, non seulement les rayons de la lumière visible, mais aussi rayons infrarouges, ultraviolets et ondes radiométriques. Les images données par les astronomes au public sont des images composites résultant de la représentation en couleurs conventionnelles de ces différents types de rayonnement.
 |  |  |
| Galaxie "Pinwheel" (M101 ou NGC 5457), appelée aussi Galaxie du Moulin ou galaxie de la roue de feu Merci à Astronoo | Galaxie du Tourbillon (M51 ou NGC 5194) A côté, son compagnon NGC 5195 Credit: NASA, ESA, S. Beckwith (STScI), and The Hubble Heritage Team (STScI/AURA) | Galaxie M88 ou NGC 4501 Crédit & Copyright: Adam Block, Mt. Lemmon SkyCenter, U. Arizona Merci à Astronoo |
 |  |  |
| Galaxie NGC 1232, dans la constellation Eridanus (la rivière) image composite d'ultraviolet, de bleu et de rouge obtenue le 21 Septembre 1998. Source ESO/VLT. Merci à Astronoo | Trio de galaxies ARP 274 Crédit: NASA, ESA, M. Livio and the Hubble Heritage Team (STScI/AURA) | Structure spirale autour de l'étoile R Sculptoris. Crédit: ALMA (ESO/NAOJ/NRAO) |
D'autres galaxies sont exposées sur la page web d'astronoo consacrée aux galaxies.
La spirale est présente aussi à l'échelle de l'étoile seule. Des astronomes ont découvert une structure spiralée autour de l'étoile géante rouge R Sculptoris, grâce au réseau d'antennes ALMA (Atacama Large Millimeter/submillimeter Array). Elle est due à de la matière (poussières, gaz, particules ionisées) qui s'échappe de l'étoile et s'éloigne en s'enroulant.
De notre Terre, nous percevons notre propre galaxie, la voie lactée, comme une trainée brillante dans le ciel. Le mot galaxie (du grec galactos) signifie justement faite de lait, car elle ressemble à une trainée laiteuse. Dans l'antiquité, les grecs racontaient que peu de temps après la naissance d’Héraklès (Hercule), Hermès l'avait placé dans le lit de la déesse Héra endormie afin qu'il la tète et devienne immortel. Alors qu'il tétait goulûment, Héra s'est réveillée et a repoussé l'enfant. Une giclée de lait du sein d'Héra s'est alors répandu dans le ciel.
Parce que la Terre est immergée dans la galaxie, nous la voyons seulement par la tranche, nous voyons son épaisseur. Depuis la Terre, la voie lactée serpente dans le ciel. Plusieurs populations autochtones ont vu dans les méandres de leurs fleuves la projection terrestre de la voie lactée. C'est le cas des Incas au Pérou avec la rivière Vilcanota (ou Wilcamayu, Huilcamayo, Urubamba) dans la vallée sacrée de Cuzco. C'est aussi le cas du Nil en Égypte, de la vallée de Tepoztlan au Mexique et de la vallée de Elky au Chili (voir Alignements de sites sacrés).
 |  |
| Voie lactée vue de la Terre | Carte du Nil |
Les données astronomiques nous indiquent que la forme de la galaxie est grosso modo un grand disque d'épaisseur variable, plus ou moins gondolé, et renflé au centre. Le système solaire y est situé à la périphérie.
Le disque galactique est structuré par des bras spiralés. Selon les dernières reconstitutions à partir des données de sondes spatiales s'élevant légèrement en-dehors de la galaxie, deux bras partent des extrémités d'une barre qui traverse le centre. Deux autres bras partent d'un peu plus à l'extérieur. Les bras des spirales sont faits d'étoiles, mais surtout de gaz et de poussières cosmiques.
 | 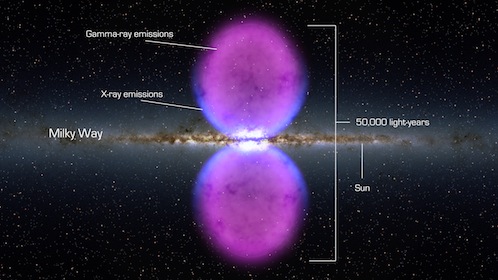 |
| La Voie lactée vue d'artiste Crédit: NASA | La voie lactée vue en tranche et son double bulbe de rayons gamma (représenté en rose) Crédit: NASA's Goddard Space Flight Center |
Des émissions de rayons gamma ont été récemment détectées. Elles s'étendent au nord et au sud du bulbe central. Leur influence s'étend sur un espace ayant la forme d'une double sphère.
Les bras spiralés de la galaxie sont en mouvement. La galaxie tourne autour de son centre. Le disque central effectue un tour complet en 26 millions d'années environ, selon les estimations des astronomes.
Mais elle ne tourne pas d'un seul bloc. A la périphérie, le soleil tourne plus lentement à la vitesse de 965 000 km/heure (250 km/s) et effectue une rotation complète en 220 millions d’années environ. C'est un peu comme lorsque vous faites tourner une crème dans une casserole en entrainant le centre avec la cuillère, l'extérieur suit plus lentement avec une inertie.
On prend habituellement comme repère le plan moyen de la galaxie, nommé le plan galactique. La rotation du soleil ne s'effectue pas strictement dans ce plan. Le soleil oscille verticalement dans la mer d'étoiles, un peu comme une balle qui flotte sur une rivière s'enfonce et reparait à la surface. C'est un mouvement sinusoïdal qui s'effectue sur un cycle de 60 millions d'années. Le soleil se situe actuellement légèrement au-dessus du plan galactique et il monte à la vitesse de 7km/s.
La trajectoire du soleil comprend aussi une vitesse proche de l'horizontale qui le déplace vers la constellation d’Hercule dans l'intérieur de la galaxie (dans la direction de l'étoile Véga) à la vitesse de 15,5 km/s par rapport à un ensemble de référence de 800 étoiles proches.
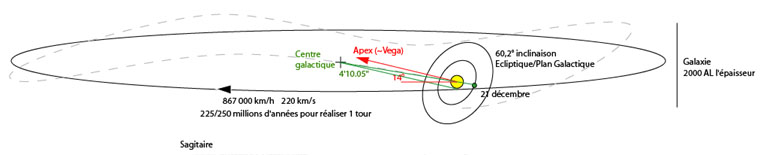 |
| Le cercle en trait continu noir représente le plan galactique. Le soleil oscille verticalement et sa trajectoire (exagérée verticalement) est représentée par le pointillé gris. Deux fois par an, le 21 juin et le 21 décembre, la Terre, le soleil et le centre galactique sont alignés Merci à U-Sphere |
Enfin, la galaxie se déplace dans son ensemble vers sa galaxie jumelle Andromède à la vitesse de 90 km/s.
Tout comme la Terre, le soleil tourne sur lui-même. Il met 27 jours pour effectuer un tour complet. Plus précisément, il ne tourne pas d'un seul bloc, comme un objet solide. Sa matière étant fluide, il tourne plus rapidement à l’équateur (en 25 jours) qu’aux pôles (en 35 jours).
Pendant que le soleil se déplace rapidement, chacune des planètes poursuit son mouvement orbital autour de lui. Le plan de l'orbite de la Terre autour du soleil, nommé plan de l'écliptique, fait un angle de 60° avec le plan galactique. Il est lié au soleil et avance avec lui.
Vous pensez que la Terre suit une orbite elliptique? C'est vrai si on considère sa trajectoire par rapport au soleil. Mais au bout d'un an, quand la Terre a effectué un tour complet de son orbite, le soleil a avancé. Il a bougé en direction de Véga (les autres mouvements sont trop lents pour qu'on en tienne compte sur quelques milliers d'années). Donc dans l'espace, la Terre décrit une hélice dont l'axe est la trajectoire du soleil.
Le cosmos est habité de matière, mais aussi d'ondes électromagnétiques et de champs magnétiques. Les champs magnétiques sont créés par des courants électriques, des particules chargées en mouvement. Toutes les étoiles sont le siège de courants de charges électriques, à la fois à l'intérieur de leur masse, et à l'extérieur, dans leur halo et des champs magnétiques s'étendent autour d'elles. On les représente graphiquement par leurs lignes de champ, qui visualisent la direction du champ magnétique en chaque point de l'espace.
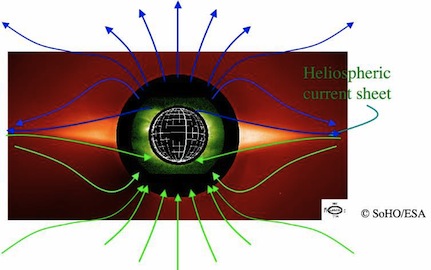
Dans le cas du soleil, des particules ionisées (électrons, protons, ions hélium) s'échappent et constituent le vent solaire. Loin du soleil, les lignes de champ magnétique sont alignées à peu près sur les courants du vent. Elles sortent par l'hémisphère nord du soleil et rentrent pas l'hémisphère sud. Les deux régions ont séparées par un plan équatorial dénommé la nappe de courant neutre ou de courant héliosphérique.
Or le soleil tourne sur lui-même et les lignes de champ ancrées à la surface suivent sa rotation. Le champ s'enroule en spirale.
 |
|
| Le courant héliosphérique, vue "de côté" Merci à nmdb | Nappe héliosphérique, spirale de Parker Crédit: J. Jokipii, Université d'Arizona |
De plus, l'axe de rotation du soleil est incliné de 7,25º par rapport au plan écliptique (orbite de la Terre) et de 67,23° par rapport au plan de la galaxie. Cela crée des vagues dans la nappe de courant neutre, qui dessinent une double spirale souvent appelée la robe de la ballerine. Son nom scientifique est la spirale de Parker du nom de l'astrophysicien Eugene Parker, qui a prédit l'existence du vent solaire en 1958 avec son champ magnétique.
Cinq planètes sont enrobées par cette spirale: Mercure, Vénus, Terre, Mars et Jupiter. Selon sa position dans le champ magnétique, la Terre peut subir des événements cosmiques et électriques plus ou moins violents.
Nous pouvons remarquer que les spirales résultent de la rotation des corps. Dans l'espace, tous les corps tournoient et se déplacent et donnent lieu à - ou sont mus par - des spirales et hélices.
De l'espace, nous dirigeons maintenant notre regard vers la surface de la Terre, plus précisément son atmosphère. Les satellites nous transmettent des images qui montrent de grandes masses de nuages qui se forment et se déplacent en mouvements complexes.
Or on y remarque assez souvent d'immenses tourbillons. Ce sont les masses nuageuses des cyclones (appelés aussi ouragans, typhons selon les régions), emportées par des vents violents atteignant jusqu'à 350 km/h.
Les cyclones se produisent surtout dans les zones tropicales. Ils couvrent des surfaces importantes et se déplacent en tournoyant. Au centre, touchant la surface de la terre, il y a une zone circulaire calme, l’œil. L'air monte en vortex.
Le mot ouragan, hurricane en anglais, huracan en espagnol, vient d'ailleurs de Hun
RaKan, un terme maya qui désigne le serpent Kan, ou Kukulkan qui se manifeste dans les nuages (voir plus loin).
Dans ce mouvement dynamique d'un vortex, on peut définir un sens réel, car contrairement à une spirale conique statique où l'on s'imagine avancer sur la spirale selon la convention de sens définie plus haut, là le mouvement est bien réel. Si l'on suit le mouvement de l'air du cyclone, son sens de rotation du cyclone est à l'inverse des aiguilles d'une montre dans l'hémisphère nord, celui des aiguilles d'une montre dans l'hémisphère sud. Vu de satellite où l'air monte vers l'observateur, on a l'apparence inverse. Cette inversion de sens d'un hémisphère à l'autre est due à la rotation de la Terre. La matière fluide liée aux corps qui tournent comme la Terre, est soumise à une force d'impulsion omniprésente, due à cette rotation (les scientifiques l'appelle la force de Coriolis).
 |  |  |
| Le cyclone Katrina, aout 2005 Merci à National Oceanic and Atmospheric Administration | L'ouragan Sandy sur la côté est des États-Unis novembre 2012 Merci à AFP PHOTO / EUMETSAT 2012 | Une tornade Merci à Dinosoria |
Les tornades sont aussi des tourbillons, mais de taille bien plus petite (exceptionnellement jusqu'à quelques centaines de mètres de diamètre). D'une durée de vie limitée (moins d'une dizaine de minutes dans la majeure partie des cas), elles parcourent rarement plus de 40 km (sauf dans le cas des tornades américaines, qui peuvent parcourir plusieurs centaines de kilomètres). La tornade soulève de la poussière et on peut voir une colonne torsadée qui s'élève dans le ciel. Cyclones et tornades ont une telle force d'aspiration qu'ils détruisent de nombreuses constructions.
La planète Jupiter est également sujette à de nombreux tourbillons dans son atmosphère. Sa Grande Tache rouge est peut-être le plus grand ouragan du système solaire. Elle est située à la latitude 19,5° qui correspond à l'un des sommets d'un tétraèdre qui, comme l'a montré David Percy, sous-tend la planète telle une ossature de courants énergétiques (voir Les sons créateurs de formes).
 |  |
| Jupiter et sa Grande Tache Rouge Crédit Nasa | Tétraèdre d'énergie sous-jacent, cause de la Grande Tache Rouge selon R. Hoagland |

Le 9 décembre 2009, le journal anglais The Sun rapporte qu'une spirale géante est apparue dans le ciel de Norvège le matin à 8h45, pendant deux minutes. Cela ressemblait à une étoile filante qui tournait en rond - et ensuite en diagonale à travers les cieux. Une queue sous forme d'un flux de rayon bleu est alors apparue pour relier la spirale à la terre, avant que la lumière «explose» en un anneau rotatif enflammé de couleur blanche. Elle a été vue par des centaines de milliers de norvégien.
L'astronome le plus célèbre de Norvège, Knut Jorgen Odegaard Roed, a déclaré qu'il n'avait jamais rien vu de tel avant la spirale. Il a affirmé: "Cela a été vu sur une surface exceptionnellement élevé du pays - dans l'ensemble du nord de la Norvège et le Trondelag. «Ma première pensée fut que c'était un météore - mais elle cela duré beaucoup trop longtemps. Il est possible qu'un missile ait été tiré en provenance de Russie - mais je ne peux pas garantir que soit l'explication." Le chef scientifique Erik Tandberg, au Centre spatial norvégien, s'est lui aussi déclaré «totalement surpris» par la spirale. Il a convenu avec les experts de nombreux autres pays que la spirale aurait pu être causée par un missile de la Russie - ce que les militaires russes ont vivement démenti. S'il s'agissait d'un missile - très probablement de la base de lancement de Pletsevsk en Russie ou à partir de l'un des sous-marins russes ou même de la base de l'Agence spatiale européenne à Kiruna -, alors il s'agirait d'un lancement de fusée qui a mal tourné. Mais je sais que les militaires ont démenti cette explication. On pourrait donc se pencher sur un phénomène naturel tout à fait nouveau."
Source : Le Post. Voir la vidéo: Spirale-céleste-aux-Infos
Des courants électromagnétiques et électriques circulent dans la terre et dans l'atmosphère. Lorsqu'on se trouve sur l'un de ces courants, soit dans des paysages, soit dans un édifice sacré, on peut ressentir une ambiance spéciale. Certaines personnes ont la capacité de les voir. Ces courants tissent un réseau dense sur la Terre, et certains ont des flux plus importants que d'autres.
D'autres courants de cette sorte s'élèvent en hélice dans l'atmosphère et pour cette raison, ils sont nommés des cheminées cosmotelluriques. Pour Georges Prat (dans son ouvrage Précis cartésien de géobiologie), les cheminées restent fixes à la surface de la Terre, sauf lorsque des changements telluriques se produisent, par des chantiers ou l'adjonction de masses métalliques.
Les cheminées respirent. Un courant monte en spirale dans le cylindre, puis un autre descend dans le même cylindre qui se contracte légèrement. Les cheminées sont des équilibreurs naturels de l'énergie de la Terre. On peut sentir la surface du cylindre avec la main, l'air y est plus dense.
Certains vortex cosmotelluriques sont créés par des éléments naturels du paysage (volcans, montagnes de forme pyramidale ou conique, confluents de rivières, chutes d'eau), ou par la présence de gisements minéraux volumineux dans le sous-sol. D'autres sont créés par la présence d'un temple construit selon les principes de la géométrie sacrée. La plupart des hauts-lieux de cette planète ont été implantés sur les croisements principaux de la grille énergétique planétaire selon des figures géométriques (voir article Alignements de lieux sacrés).
Dans les vortex des croisements principaux, la sensation y est plus forte. Lorsqu'on y séjourne un moment, on peut ressentir leur présence par des effets spéciaux sur le corps et l'esprit. Cela peut être tout simplement un sentiment de bien-être et de beauté. Certains nous mettent dans des états mentaux modifiés tels que l'impression d'être ailleurs, comme en rêve. On peut aussi être pris de vertiges.
Les vortex de haute énergie sont parfois le lieu de phénomènes étranges. Ils provoquent des distorsions magnétiques et gravitationnelles mesurables. Un ingénieur canadien, Wilbert Smith, a étudié scientifiquement un de ces vortex, celui de Marysburgh dans le Lac Ontario au Canada (Project Magnet). Il a mesuré les perturbations gravitationnelles et conclu que les colonnes de ce vortex ont un diamètre d'environ 300 m et une hauteur de plusieurs km, avec une localisation un peu fluctuante.
Descendons plus encore jusqu'à la surface de la Terre. Des spirales et des méandres y sont abondamment présents dans les cours d'eau.
Les rivières préfèrent naturellement les courbes sinueuses. Elles serpentent selon des tracés variés, soit en méandres, soit en tresses lorsque plusieurs petits bras se recoupent. Elles suivent très rarement un tracé rectiligne. Les portions rectilignes ne dépassent pas 10 fois leur largeur. Elles se produisent dans des circonstances contraignantes: en cas de pentes très fortes où elles deviennent des torrents, ou en présence de lignes de faille.
 |  |  |
| Méandres Merci à Buzzle | L'Amazone Merci à Alice & Emily | La Sioule, en Auvergne. Méandre vu de la commune de Queuille Merci à Jim L'Auvergnat |
En laboratoire, des ingénieurs ont simulé le développement naturel d'un cours d'eau dans un lit de sable et ont découvert qu'il tend à se développer en méandres.
Lorsque les ingénieurs redressent le lit d'une rivière en modifiant les berges, ils disent qu'ils le rectifient, c'est-à-dire qu'ils le rendent droit. C'est juste, mais le mot rectifier a un autre sens, c'est remettre dans le droit chemin. Or cette rectification selon les règles en vigueur de la pensée humaine mécanique est plutôt nocive pour la rivière, et elle a souvent des conséquences hydrologiques et écologiques désastreuses.
 | 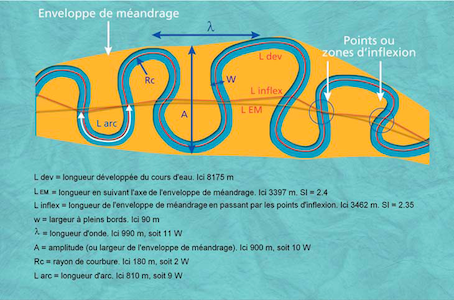 |
| Expérimentation de Gardner (1973) Merci à J-R Malavoi et J P Bravard | Méandrage Merci à J-R Malavoi et J P Bravard |
Des chercheurs se sont intéressés à la géométrie des rivières. Ils ont trouvé qu'elles suivent des lois de proportion assez précises. A l'échelle près, tous les bassins des rivières se ressemblent quelle que soit leur étendue. Ils ont les mêmes formes arborescentes ou ramifiées, que ce soient de petits ruisseaux ou de grands fleuves. Les petits cours d'eau se jettent dans des cours d'eau plus larges qui se rassemblent en un fleuve. Cette structure est dite fractale (voir article Images fractales).
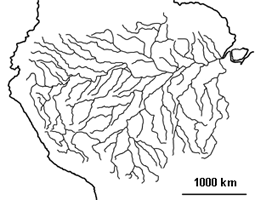 | 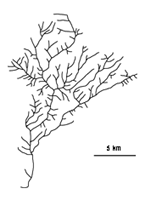 |
| Les réseaux fluviaux ont la même forme arborescente, qu'on les observe à l'échelle de milliers de kilomètres (à gauche réseau de l'Amazone) ou à celle de quelques kilomètres (à droite réseau du Sabino en Arizona) D'après C. Allègre, Sciences et Vie, 1995 | |
Précisions mathématiques sur les mesures: Les méandres sont proportionnels à la largeur du cours d'eau. Par exemple, leur rayon de courbure (Rc) vaut environ 2 à 3 fois la largeur de la rivière. La distance entre 2 méandres voisins (longueur d'onde λ) est généralement comprise entre 7 et 11 fois la largeur. L'amplitude entre deux boucles opposées vaut environ 10 à 12 largeurs, ou encore 2,5 λ. La largeur elle-même est proportionnelle au débit entrant, lui-même proportionnel à la superficie du bassin.
Les méandres se déplacent lentement par l'érosion d'une rive et le remblaiement de l'autre par l'action des courants. Un courant se dirige transversalement en surface vers la courbe extérieure du méandre (la rive concave) et plonge vers le fond en la creusant, puis revient vers la rive convexe où il dépose ses charges alluviales. Le courant transversal suit donc une trajectoire hélicoïdale.

Des observations minutieuses des courants des rivières ont été effectuées dès les années 1930 par Viktor Schauberger (1885 - 1958), un garde forestier au service d'un prince autrichien. Il passait de longues heures à contempler la forêt et l'eau. Ses conclusions sont révolutionnaires et encore peu connues. Il indique que la température des courants a une importance primordiale. Les rives étant exposées différemment au soleil selon leur orientation et l'ombrage des arbres, les courants qui les longent ont des températures et donc des vitesses différentes. C'est cette différence de vitesse qui les force à se courber et qui crée les méandres.
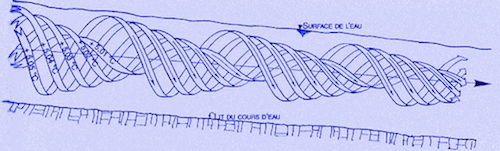
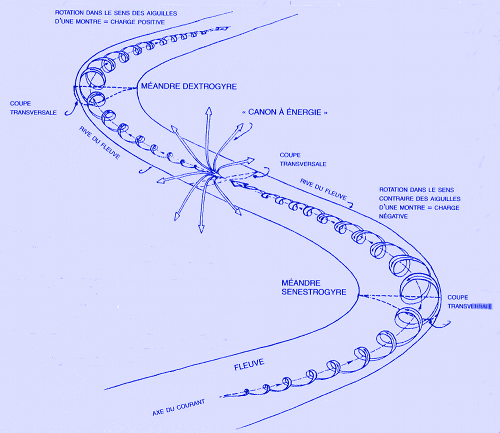
Extrait de V. Schauberger, cité par A. Bartholomew
Le courant longitudinal est organisé en couches de températures différentes. Les couches périphériques sont très légèrement plus chaudes que celles du centre (quelques centièmes de degrés). Le sens de rotation est à droite dans les méandres qui tournent à gauche et à gauche dans les méandres qui tournent à droite.
Le flot naturel en hélice donne plus de force à l'eau. Schauberger a démontré la réalité de cette force en 1922 en construisant des canaux de flottaison pour transporter des grumes (tronc d'arbres). Les berges du canal ont été équipées de rainures en spirales afin d'imprimer à l'eau un mouvement hélicoïdal. Cela augmente sa force de portée et permet de transporter des grumes trop lourdes pour passer dans les constructions rectilignes classiques.
Lorsqu'on contraint un cours d'eau à passer entre des rives droites bétonnées, il perd son mouvement hélicoïdal et sa dynamisation. Dans ce cas, il a une plus forte tendance à sortir de son lit et à inonder les terrains riverains. On peut donc facilement réduire les risques d'inondation en redonnant à la rivière son cours sinueux naturel.
Schauberger a mis en évidence l'importance du gradient de température entre les couches du courant hélicoïdal, gradient tellement faible qu'il est négligé par les hydrologues. Pourtant il est la cause essentielle du bon fonctionnement de la dynamique du flux. L'ombrage des rivages participe à l'établissement de ce gradient.
En respectant ces caractéristiques naturelles des courants, on peut les aménager de façon intelligente. Selon V. Schauberger (Unsere
sinnlose Arbeit - Die Quelle des Weltkrise, 1933), "On peut régulariser les cours d'eau sur n'importe quelle distance sans édifier de remblais; transporter du bois d’œuvre et autres matériaux, même s'ils sont plus lourds que l'eau, tels que minerais, pierres, etc. en profondeur et dans l'axe du courant; remonter le niveau des nappes phréatiques dans la campagne environnante et enrichir l'eau de tous les éléments nécessaires à la végétation dominante...
Il est ainsi possible de produire artificiellement une eau potable de qualité pour humains, animaux et plantes, mais en répondant aux critères de la nature; de rendre le bois d’œuvre et autres matériaux analogues ininflammables et imputrescibles; de faire monter l'eau dans un tuyau vertical sans avoir recours à des pompes; de produire n'importe quelle quantité d'électricité et d'énergie rayonnante presque gratuitement; d'améliorer la qualité du sol et de guérir cancer, tuberculose et pathologies nerveuses...
En appliquant ces lois nouvellement découvertes, je suis déjà l'auteur de quelques réalisations d'envergure destinées au flottage du bois, à la régularisation des cours d'eau, et qui fonctionnent parfaitement depuis une décennie, déconcertant aujourd'hui les spécialistes en hydraulique."
L'eau tourbillonne dans la mer comme dans les rivières, sous la force des vagues. Le tsunami du 11 mars 2011 au Japon a créé d'immenses tourbillons sur lesquels un bateau semblait un fétu de paille.
 |  |
| Vortex dans une bouteille © JL Naudin | |
 | |
| Tourbillon à Ibaraki lors du tremblement de terre au Japon le 11 mars 2011 Merci à Kampaï | Spirale à 14 bras formée dans l'eau d'une coupe soumise à une vibration sonore de 102,528 Hz © A. Lauterwasser, Images sonores d'eau, éd. Médicis, 2005 |
Des tourbillons se forment naturellement dans l'eau pas seulement dans les rivières, mais également chaque fois que l'eau peut s'écouler naturellement. Le jet d'eau du robinet sort en tournoyant. Des tourbillons se forment au fond d'un évier qui se vide. Lorsqu'un jet d'eau tombe dans de l'eau, il se forme un vortex. (voir film en annexe)
Des tourbillons sont susceptibles de se produire dans tous les fluides, que ce soient des liquides comme l'eau, des gaz comme l'air, ou des poudres de fines particules telles que du sable fin, du sel fin ou du pollen. Lorsqu'on soumet de tels fluides à l'influence de vibrations mécaniques, particulièrement de vibrations sonores, la poudre ou l'eau se déplacent et s'organisent. À certaines fréquences, de belles figures géométriques apparaissent. Certaines d'entre elles contiennent des spirales multiples (voir détails dans l'article Les sons créateurs de formes).
Quittons l'observation courante à la surface de la Terre et continuons à descendre dans l'échelle de nos observations du monde naturel.
Nous voici à l'intérieur du corps humain où nous examinons le système sanguin. Comme dans les rivières, le flux sanguin suit un mouvement hélicoïdal dans les artères et les veines. Cela a été vérifié par imagerie dans l'aorte ascendante et descendante. L'impulsion de rotation est fournie par la structure de la paroi de l'artère.
Des chercheurs ont reconnu qu'un flux hélicoïdal est beaucoup plus dynamique qu'un flux linéaire. Ce fait est mis en évidence dans les prothèses d'artère. Les prothèses cylindriques classiques s'encrassent vite, alors que dans les prothèses hélicoïdales, il ne reste pas de zones stagnantes, ce qui réduit les risques d'hyperplasie intime et d'athérosclérose.
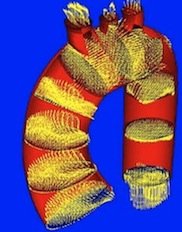 |  | 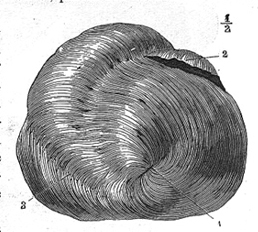 |
| Flux hélicoïdal dans l'aorte humaine ascendante. Merci à Jin Suo | Prothèse artérielle hélicoïdale conçue par le professeur CG Caro Merci à Imperial College de Londres | Fibres musculaires à la base du cœur Merci à IRM cardiaque |
Le cœur, pièce maitresse du système sanguin, imprime au flot sanguin des mouvements de vortex dans ses cavités internes. Cela est assuré par la disposition en hélice des fibres musculaires qui constituent la paroi du cœur. On remarque particulièrement la structure hélicoïdale de la pointe du cœur.
Sources: Recueil d'IRM cardiaque, Rotations et torsions liées à l’architecture complexe des fibres myocardiques; The Dynamic Heart and Circulation, Craig Holdrege, The Nature Institute, In context n°7, 2002, pp. 15-18; Torsional Ventricular Motion and Rotary Blood Flow, Frank A. Baciewicz Jr., David G. Penney, William A. Marinelli, and Ralph Marinelli. Current concepts in cardiac dynamics, aout 1991
D'autres spirales structurent certaines parties de notre corps. La peau de l'extrémité de nos doigts est dotée de dessins extraordinaires, les empreintes digitales. Elles sont uniques à chacun, au point qu'elles sont utilisées comme marques d'identification. On y remarque nettement des lignes enroulées en spirale. La spirale se divise en bifurcations à plusieurs endroits qui sont particuliers à chacun.
Dans l'oreille interne, la cochlée a pour rôle de percevoir et de distinguer les fréquences sonores. Elle est aussi appelée limaçon en raison de sa forme tubulaire enroulée en spirale plane.
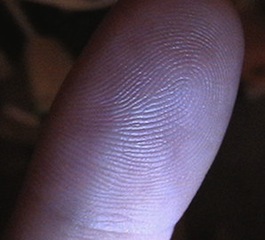 |  | 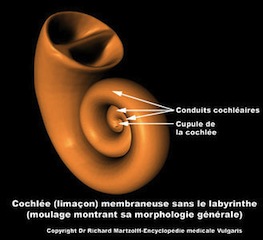 |
| Empreintes digitales | Empreintes digitales Merci à Biométrie | Cochlée dans l'oreille interne © R. Martzolff - Encyclopédie médicale Vulgaris |
Toujours dans le corps, la spirale est présente au niveau moléculaire dans la célèbre molécule d'ADN ainsi que dans les molécules de protéines.
L'ADN est constitué de 2 brins enroulés en hélice. Cette hélice tourne à droite (voir L'ADN et le code génétique). Des chercheurs allemands et russes ont découvert que l'ADN stocke les rayons lumineux qu'il reçoit en provenance des autres cellules. Il en réémet selon des processus quantiques élaborés. Les rayons émis portent des informations qui sont distribuées aux autres cellules, de sorte que le corps a une vision globale de lui-même à tout instant. Les informations sont inscrites dans la polarisation de cette lumière, c'est-à-dire la façon dont l'onde tourne de façon hélicoïdale. Une partie de ces informations constitue un code génétique électromagnétique, qui se superpose, complète et supervise le code génétique moléculaire (voir article L'ADN électromagnétique).
Les molécules de protéines sont également constituées d'une chaine d'éléments, ces éléments étant les acides aminés. Or cette chaine se replie dans certains parties et peut alors prendre deux types de configuration: soit elle est repliée en accordéon (les biologistes nomme feuillet béta cette structure), soit elle est enroulée en hélice (hélice alpha). Une protéine est donc faite d'hélices alpha et de feuillets bêta reliés par des segments qui n'ont pas de structure secondaire particulière.
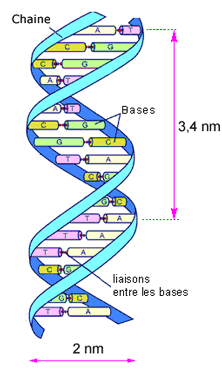 | 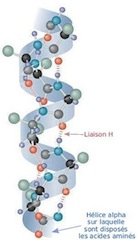 |
| Schéma de l'ADN Merci à JJ Wawrzyniak | Configuration d'une chaine de protéine en hélice alpha Merci à Wikipédia |
Dans l'observation microscopique des organismes, nous découvrons que les molécules de certaines substances organiques tels que le cholestérol et ses dérivés ont des formes allongées torsadées. En s'empilant, elles se disposent en arrangements hélicoïdaux périodiques. Ces substances sont appelées des cristaux liquides cholestériques (voir article Cristaux liquides). Lorsqu'on les étale en couche mince sur une surface plane, les couches forment souvent des enroulements spiralés.
 | |
| Schéma de la structure cholestérique Les molécules s'empilent en tournant. ©Dessin A. Boudet, CNRS éditions | Spirales dans un cholestérique Microscopie électronique en transmission © Cliché A. Boudet, CNRS éditions |
Notre descente vers le microscopique n'est pas terminée. Après notre parcours depuis les galaxies jusqu'aux molécules en passant par les rivières, les plantes, les animaux et l'homme, nous allons découvrir l'hélice et la spirale dans les structures les plus fondamentales de l'univers, les particules élémentaires.
Selon de nombreux scientifiques d'avant-garde, l'espace n'est pas vide. La théorie qui a déclaré au 20e siècle que l'éther n'avait aucune existence n'est pas cohérente. Afin d'expliquer certains phénomènes, il est nécessaire de supposer l'existence d'un fluide primordial qui remplit l'espace et pénètre toute matière. C'est ce que les anciens appelaient l'éther, et on peut lui attribuer à nouveau ce nom. Dans d'autres traditions, il est nommé prana, chi ou akasha.
Le scientifique américain Hal Puthoff a montré que le "vide" du zéro absolu (-273°C) contient une énergie faramineuse qui n'est pas de nature électromagnétique. C'est ce qu'on nomme l'énergie du point zéro.

Un des pionniers dans ce domaine a été l'astrophysicien russe Nikolai Alexandrovich Kozyrev (1908 – 1983), dont les travaux ont longtemps été tenus secrets dans l'Union soviétique. À la suite de très nombreuses expériences, il a démontré que les objets sont imprégnés de cet éther et qu'ils peuvent soit déverser, soit aspirer une partie de cet éther dans certaines conditions mécaniques et thermiques. Les flux d'énergie s'écoulent par des mouvements spiralés nommés champs ou ondes de torsion. D'autres scientifiques les ont nommés ondes scalaires. (voir mon article L'éther fluide et tourbillonnaire des champs de torsion)

Un autre chercheur russe émigré aux USA, Vladimir Ginzburg avance que les atomes n'ont pas une réalité matérielle par nature. Les atomes et molécules sont des vortex d'éther localisés. C'est donc comme une agglomération, un enroulement plus dense de l'éther. En fait, les atomes et le prétendu vide sont faits de la même étoffe, l'éther.
Dans les modèles de Charles Crane, Harold Aspden et d'autres, les particules tournent en se déplaçant, ce qu'on nomme le spin. L'axe de rotation de ce spin s'aligne sur la direction de déplacement. Dans un volume sphérique, le vortex se forme le long de l'axe de rotation, créant une sorte de tunnel central. Les flux montent du pôle sud vers le pôle nord, et reviennent par l'extérieur en coulant le long de la sphère.
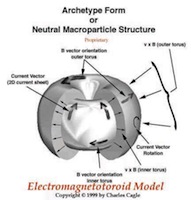 |  | 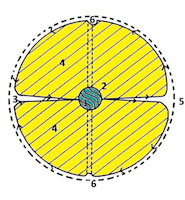 | 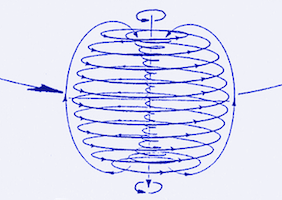 |
| Modèle quantique électro-magnétotoroïdal de Ch. Cagle Merci à D. Wilcock | Le modèle de double tore des particules selon Nassim Haramein | Modèle bihémisphérique des particules selon O. Boa (Luminance, Ariane 2012) | Vision de V. Schauberger: les mouvements d'énergie en vortex forment les particules. |
Dans cette ligne de pensée, le physicien Nassim Haramein a développé, par un raisonnement déductif rigoureux accompagné de publications scientifiques (voir la page Publications scientifiques de ce site), un modèle de double tore, où les deux hémisphères tournent en sens opposé. Sur la surface extérieure du tore, les flux adoptent un trajet hélicoïdal.

Olivia Boa est une jeune femme étonnante qui, sans être spécialiste de la physique, est passionnée par la constitution de l'univers et par l'épanouissement spirituel des êtres humains. En conscience modifiée, elle a la capacité de recevoir des informations de physique avancée, sous forme d'instructions et d'images. C'est ainsi qu'elle a énoncé un modèle qui serait le mécanisme fondateur de toute particule. Là encore, on a deux hémisphères qui tournent en sens opposé, et selon leur vitesse, apparaissent sous forme de particules différentes. De plus cette particule possède une structure interne divisée en 5 parties.
Ces théories de physique fondamentale seront examinées plus en profondeur dans un autre article.
V. Schauberger avait eu une intuition analogue en contemplant l'eau. Pour lui, la spirale est à la base de tout mouvement de vie, depuis le niveau particulaire jusqu'aux galaxies. Le mouvement naturel de l'énergie est de se propager en spirale, non en ligne droite. Lui aussi avançait que ce sont des mouvements d'énergie en vortex qui créent la matière.
Des spirales sont présentes à tous les niveaux de l'Univers. depuis les galaxies lointaines jusque dans l'atome, en passant par les plantes, les animaux, les minéraux, et les molécules de notre corps. Elles se partagent la vedette avec les polygones et les polyèdres. Ensemble, ils démontrent que les objets de l'univers sont sous-tendus par des trames géométriques.
Nous en explorons le sens et les implications dans l'article
Aspects géométriques et sonores des créations de l'univers.
Examinons maintenant la place de la spirale dans la vie culturelle, psychique et spirituelle des hommes.
Inscrite au plus profond de la structure de la matière, y compris dans les champs énergétique de l'espace, la spirale préside à la création des mondes, que ce soit à l'échelle des atomes comme à celle des galaxies. Elle est une structure dynamique sous-jacente dans la manifestation de toutes choses.

Le papillon Galactique Hunab Ku
Représentation du dieu/déesse de la création chez les Mayas.
Merci à Mayan Prophecy
Il n'y a donc rien d'étonnant à ce que la spirale ait été représentée et honorée dans les civilisations du monde entier. Elle y exprime la force fondamentale à la base de la Vie et de la Création. Elle est la force vitale de tous les êtres, qui leur permet de grandir, de se développer et de se déployer. Elle représente aussi la conscience qui crée cette Vie.
Pour les anciens Mayas, le Créateur/créatrice était Hunab Ku, le Papillon Galactique, localisé au centre de notre Galaxie. Hunab Ku représente la conscience qui existe en toute chose dans notre Galaxie. Elle est la Matrice Divine qui donne naissance aux étoiles et aux planètes, qui a donné naissance au soleil et à notre Terre. Elle est à l'origine des impulsions de nouvelles formes de conscience sur la Terre qui se produisent périodiquement selon le calendrier maya, par émanations d'énergie en provenance du centre de la galaxie. Hunab Ku est représenté par une spirale assortie des antennes et des ailes du papillon.
La spirale a été représentée dans les monuments mégalithiques dans de nombreux lieux de la Terre. Dans l'ile de Gavrinis (France, Morbihan), se trouve un tumulus, le cairn de Gavrinis, qui recouvre une chambre et un couloir fait de pierres plates mégalithiques à la façon d'un dolmen. Or ces pierres ne sont pas seulement des parois, mais aussi le support de nombreuses gravures. 21 dalles d'entre elles sur 29 sont ornées de nombreuses spirales.
En Irlande, on retrouve le même style de construction mégalithique à Newgrange (Sí an Bhrú) à proximité de la vallée de la Boyne (site de Brú na Bóinne). Le tumulus le plus spectaculaire inclut un couloir conduisant à une chambre. On y a découvert une pierre posée à terre à l'entrée, sur laquelle sont gravées des spirales dont certaines sont groupées par trois.
 |  |  |  |
| Cairn de Gavrinis. Une pierre du couloir Merci à Ancient Wisdom | Pierre à l'entrée de Newgrange Merci à Wikipedia | Spirales et serpents sur les deux faces d'une plaque en os de mammouth, Mal'ta, Sibérie | |
L'association de trois spirales est connue sous le nom de triskèle, triskel, triskell, triquètre, ou triscèle, qui en grec signifie à trois jambes. Bien que le triskèle soit apparu dans diverses cultures et à différentes périodes, il est considéré comme une caractéristique importante de l'art celtique. Récemment, il a été choisi comme symbole de la culture bretonne.
Les spirales sont aussi représentées sur des objets. Dans la culture Mal'ta, qui a vécu vers 21000 à 17000 avJC près du lac Baïkal en Sibérie, on a mis à jour une plaque en os de mammouth, de taille 13,8 par 8,1 cm. Sur une des faces, est gravée une spirale faite de petits trous, entourée de spirales plus petites. Sur l'autre 3 serpents.
À Towie, en Écosse, dans la région d'Aberdeen, on a découvert de curieuses petites boules en pierre, au nombre de 411 toutes différentes, de la taille approximative d'une balle de tennis. On les date à environ 3000 avJC. Leur forme se rapproche de polyèdres, particulièrement du cube, avec 6 disques proéminents, sur lesquels sont gravées des spirales.
 |  |  |  |
| Boule gravée de Towie, Écosse Merci à Ancien Crafts | Mosaïque dans une villa romaine, Corinthe Merci à anthopologieenligne | Crosse d’évêque dite du chancelier Guérin, 2e quart du XIIe siècle Merci à Wikipédia | Van Gogh Nuit étoilée Merci à Wikipédia |
Avançant à une époque plus récente, nous rencontrons des mosaïques romaines, comme celle-ci de Corinthe au 2ème siècle après J.C. À partir du 12e siècle, le bâton des évêques chrétiens, la crosse, a pris la forme spiralée. La spirale inspire de nombreuses œuvres d'art contemporaines, comme si elle était inscrite dans notre inconscient. Telle cette toile de Vincent Van Gogh, Nuit étoilée (1889).
Le principe de la Vie a été représenté sous la forme du serpent et vénéré dans nombreuses traditions (égyptienne, babylonienne, celte, védique, chinoise, amérindienne, amazonienne, aborigène, océanienne, africaine...).
Les représentations de serpents mettent en scène deux types opposés de symboles, l'une positive, l'autre négative. Dans sa forme négative, le serpent est perfide et trompeur, comme dans la Bible ou les récits sumériens. Il exprime les forces terrestres séparées du divin, qui cherchent le pouvoir pour elles-mêmes. Ces forces sont extérieures à nous, mais aussi intérieures. Ce sont nos désirs de pouvoir sur les autres, et toutes nos émotions négatives de jalousie, vengeance, ressentiments, sous-estime de soi, etc (voir article L'enfant intérieur).
 |  |  |
| Le dieu Kukulcan Site archéologique maya de Yaxchilan Mexique Merci à Musées Nationaux | Intérieur du sarcophage de Tachapenkhonsou Égypte, vers 700 av. J.C. Paris, musée du Louvre Merci à Histoires de serpents | Python Arc-en-ciel Yurlungur (Julunggul) selon les aborigènes d'Australie) Lyon, musée des Confluences Merci à Histoires de serpents |
Dans son aspect positif, le serpent s'élève vers le ciel. Il est alors doté d'ailes, comme le dieu Quetzalcoatl de la Mésoamérique, le serpent à plumes, appelé Kukulkan (ou Kukulcan) chez les Mayas. Il est le dieu générateur qui rétablit (redonne en tant que rédempteur) la vie divine des origines.
Le serpent cosmique vénéré n'est pas conforme à un serpent biologique terrestre. Il est souvent représenté avec deux têtes, deux pieds, et/ou deux ailes. Il est parfois tellement gigantesque qu'il peut entourer la terre (Voir J. Narby, Le serpent cosmique). On le voit s'élever vers le ciel en s'enroulant sur un pilier. Le pilier est l'axe du monde, représenté également sous forme de bâton, de corde, d'échelle ou d'arbre.
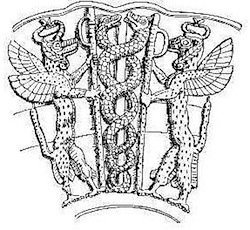 |  |  |  |
| Représentation du dieu sumérien Ningishzida sous la forme de 2 serpents entrecroisés. Il représente l'arbre de vie, surveillé par 2 griffons Gravure sur vase de libation, antérieur à 2000 avJC. Merci à Wikimedia | Nagakal (pierre -serpent), Inde (C) RMN-Grand Palais merci à Musées Nationaux | Le caducée symbole de connaissance chez les égyptiens | L’œuf cosmique selon Jacob Bryant (1774) Merci à wikimedia |
Le serpent peut être dédoublé afin de représenter les 2 polarités, masculine et féminine. Chez les Égyptiens, ce symbole est devenu le caducée, porté par le Dieu Thot (Hermès chez les grecs).
Le monde est l’œuf cosmique appelé œuf orphique chez les grecs. Ce symbole décrit aussi une réalité de flux énergétiques s'écoulant de l'univers sur la Terre et sur les autres planètes. Des chamanes peuvent percevoir cette forme cosmique sous l'apparence d'une sphère (l’œuf) traversée par un double entonnoir (l'arbre ou le pilier) qui passait dans le soleil. C'est exactement la forme du double tore des particules élémentaires décrit plus haut.
Selon le contexte, on peut considérer que la spirale et le serpent sont des aspects féminins de la création, tout en courbes, générateurs de vie. Il existe aussi un aspect masculin, qui s'exprime sous forme de systèmes de lignes droites et de polyèdres (l'aspect géométrique de l'univers sera développé dans un autre article). Les deux agissent en synergie et en harmonie.
L'être humain est construit à l'image de l'univers. Selon la formule du dieu Thot/Hermes, ce qui est en bas est comme ce qui est en haut. Le caducée représente donc aussi l'énergie (la kundalini) qui monte le long de la colonne vertébrale des humains le long de 3 canaux, le canal central et deux canaux spiralant autour du canal central.
Grâce au travail spirituel de la personne en quête de sa réalisation, l'énergie monte le long des canaux. Les circuits se croisent dans les centres énergétiques ou chakras et les réactivent, leur redonnant leur plein potentiel. Finalement, ils s'épanouissent au sommet de la tête, marquant ainsi la réalisation complète de l'être et sa reconnexion avec les plans supérieurs de lumière (voir article Chakras et corps subtils). Alors, il sait maitriser ses pensées et ses actes, et il a accès à toute la connaissance de l'univers. Il est devenu un initié, dont le caducée est le symbole.
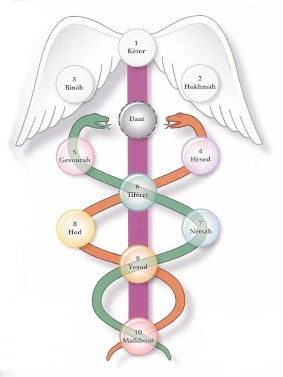 |  |
| Les énergies ida et pingala le long de la colonne vertébrale. Merci à Neoconscience | Le symbole Yin et Yang Merci à Wikimedia |
De façon analogue, le symbole taoiste du yin et du yang exprime l'équilibre entre les deux polarités, équilibre existant préalablement dans l'univers. Mais l'équilibre a été dérangé sur terre et dans les êtres, et le retrouver nécessite un travail de reconnexion. Les points montrent qu'une polarité n'existe jamais toute seule. Elle est toujours en équilibre avec l'autre. Il est nécessaire d'équilibrer les deux polarités à tous les niveaux. Le symbole peut être vu comme la stylisation de deux serpents qui s'enroulent l'un autour de l'autre.
Alors que les serpents sacrés représentent le développement de la vie dans son axe vertical vers les plans supérieurs, les spirales planes représentent le déploiement de cette force de vie dans sa manifestation extérieure. Elles invitent à l'expression de notre moi profond, véritable, non un moi artificiel piloté par l'apparence (voir article Spiritualité et développement).
Par sa racine, le mot spirale lui-même indique ce sens. Il est dérivé de spire qui vient du latin spira et du grec σπεῖρα qui signifient tour, enroulement, anneau de serpent. Spira a donné spirare, qui signifie souffler et spiritus le souffle. Le souffle, c'est à la fois le souffle de l'air, mais aussi celui de l'esprit. D'où inspirer, inspiration, et spirituel. Quant au mot volute qui vient de tourner (cf révolution), on le retrouve dans évoluer.
Si nous voulons nous extérioriser, nous devons partir de notre centre. Or, à cause de notre vie, nous nous sommes éloignés de notre centre, nous nous sommes dispersés, nous avons perdu le sens de notre vie (voir article L'enfant intérieur). Nous nous trouvons à l'extérieur de la spirale et nous devons en retrouver le centre.
Au cours de notre vie, nous parcourons la spirale dans les deux sens. De l'extérieur vers le centre, nous nous reconnectons à notre Essence, notre Principe de Vie. Lorsque nous la parcourons du centre vers l'extérieur, elle représente notre programme de Vie qui se déploie dans sa modalité propre pour donner forme à un être pleinement épanoui. Elle représente l'accomplissement de soi.
Notre parcours de vie en spirale peut aussi être concrétisé dans la matière, par un mouvement réel. Le jeu de l'oie en est une façon traditionnelle. Souvent rabaissé comme digne d'intérêt seulement pour les enfants, c'est un jeu initiatique qui a un long passé. Fulcanelli a écrit qu’il s’agissait d’un labyrinthe populaire de l’Art sacré, et [d’un] recueil des principaux hiéroglyphes du Grand Oeuvre.

On pense que le premier jeu de l'oie sous sa forme actuelle date de 1640, mais il a eu des ancêtres, comme le jeu de Dédale ou le jeu égyptien du serpent. Son parcours est une spirale parsemée d’embuches, et le joueur s'efforce d’en atteindre le centre, son propre centre, sa divinité. Parmi les embûches, il y un puits, une prison, la mort et un labyrinthe. Mais il y a aussi des impulsions bénéfiques, ce sont les oies. Tantôt on avance et tantôt on recule.
L’oie est un animal intéressant par plusieurs aspects. Phonétiquement, il est très proche de l'ouïe, surtout à la façon dont on prononçait autrefois le mot oie [oué]. Justement, la cochlée de l'oreille est aussi une spirale. Il s'agit d'écouter.
L'oie, en marchant, claudique. C'est le pas de l'oie, une sorte de boitement. Nous boitons parce que nous ne sommes pas encore d'aplomb et nous cherchons notre axe.
Une boiteuse célèbre a été la reine Pédauque, dont le nom signifie Pied d'oie, pé d'auca (prononcé aouco) en patois occitan ! Sa réalité historique est incertaine, mais elle a longtemps été considérée comme étant Austris, la fille du cinquième "roi" de Toulouse, Marcellus, très belle, mais qui a été enlaidie par la lèpre. Toulouse était alors la capitale du royaume wisigoth (de 413 à 508) que les fervents du christianisme nouveau appelaient les païens. En secret, Austris développa une grande piété pour le Christ avec l'aide de St-Saturnin et fut guérie. Mais ses pieds restaient probablement déformés.
L'empreinte du pied d'oie est composée de 3 barres divergentes, qui représentent aussi la divinité, la trinité.
Le jeu de la marelle est un autre jeu initiatique ancien, qui a une fonction analogue à celle du jeu de l'oie avec un parcours à effectuer. La différence est que le joueur passe de son état à terre à un état relié au ciel en poussant une pierre (son âme) avec son pied.
Ce qui est intéressant, c'est que tout le corps participe à ce parcours, et la mémoire de cette expérience est ainsi imprimée dans les cellules. Remarquons qu'on effectue ce parcours en sautant sur un pied (à cloche-pied), en claudiquant.
D'où vient ce nom? Peut-être de mérelle, mère de la lumière? C'est le nom donné à la coquille du pélerin de Compostelle, qui effectue un parcours bien physique, guidé par sa coquille, et s'efforce d'atteindre le champ des étoiles (compo-stelle).
Nous nous sommes momentanément éloignés de la forme spirale, et pourtant la marelle est parfois tracée sous la forme d'un escargot. Dans l'antiquité, la marelle était un labyrinthe. Dans le tracé des labyrinthes, nous allons retrouver un autre parcours initiatique en forme de spirales plus élaborées.
Dans la tradition des labyrinthes, nous trouvons également un parcours initiatique qui nous conduit d'abord vers le centre puis vers l'extérieur. Habituellement, quand nous parlons de labyrinthes, nous pensons d'abord aux labyrinthes de loisirs, labyrinthes de foire, labyrinthes végétaux, qui sont des dédales à plusieurs chemins dont un seul conduit vers la sortie.
Mais les labyrinthes initiatiques sont bien plus anciens et sont construits selon un autre principe. Il n'y a qu'un seul chemin, une seule voie et aucun risque de s'y perdre. Au contraire, on s'y trouve. Ils sont tracés sur le sol ou bâtis en grands édifices. On les parcourt en marchant lentement, et comme pour la marelle, ça passe par la mémoire corporelle et énergétique. Chaque pas est fait en conscience.
Où trouve-t-on ces labyrinthes? Partout dans le monde, à commencer par les grandes cathédrales françaises comme Chartres ou Amiens. La cathédrale de Reims en était aussi équipée, mais les enfants y jouaient souvent, et comme chacun sait, ils font du bruit et ça dérange les autorités. Aussi l'autorité ecclésiastique de l'époque (1778) l'a-t-elle fait détruire.
 | |
| Labyrinthe de la cathédrale d'Amiens Merci à Wikimédia | Cathédrale de Reims. Le labyrinthe reconstitué par une projection lumineuse à l’occasion du 800e anniversaire de la cathédrale, du spectacle “Rêve de Couleurs” par la compagnie Skertzo. Merci à Christian Claudel |
En Scandinavie, les labyrinthes sont très courants dans les églises, dessinés sur la paroi ou au plafond, ou réalisés en fresque (dans du plâtre frais). En Suède, Norvège et Finlande et tout le nord de l'Europe, des labyrinthes sont tracés sur le sol dans la nature. Des pierres délimitent les allées. On compte plusieurs centaines de ces labyrinthes de pierres dans les régions situées au-dessus du cercle polaire.
Ils sont désignés sous le nom de Trojeborg, qui signifie ville de Troie, ville célèbre dans l'épopée grecque pour la guerre de Troie et le cheval de Troie, dont le lieu se situe dans la Turquie actuelle. Le plan de cette ville aurait été un véritable dédale. Même chose en Angleterre où on trouve de nombreux jeux de Troie.
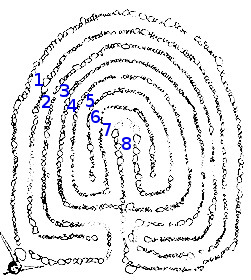 | 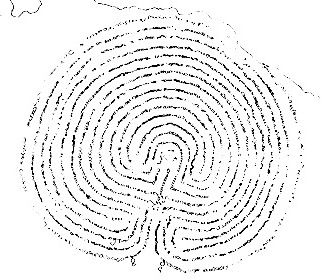 |
| Labyrinthe en pierres à Lindbacke, Suède Croquis de Ivar Schnell, 1934 Merci à Labyrinthos | Labyrinthe de Tibble, Suède Croquis de John Kraft, 1980 Merci à Labyrinthos |
Nous remarquons que le chemin ne suit pas une spirale simple. On tente de s'approcher du centre et on y va apparemment d'abord rapidement. Si on numérote les circonvolutions de l'extérieur vers l'intérieur, par exemple sur un labyrinthe classique à 7 circonvolutions plus le centre, on entre directement à la spire 3. Mais ensuite on s'éloigne du centre et on revient à la 2. Le parcours se fait dans l'ordre 3 2 1 4, puis 7 6 5 8 (voir ouvrage Les labyrinthes, S. Lonegren).
Ce schéma existe depuis très longtemps. Il est représenté sur une tablette d'argile de la ville mycénienne de Pylos. Mais il semble beaucoup plus ancien, peut-être au moins 4000 ans av.JC. En Crète, il a été forgé sur les monnaies de Cnossos, en lien avec le labyrinthe construit par Dédale qui abritait le Minotaure.
 |  |  |  |
| Labyrinthe sur une tablette d'argile, vers 1200 avJC Merci à Wikipédia | Pièce de monnaie de Cnossos, Crète, vers 280 avJC Merci à M.K. Dewitt | Labyrinthe gravé sur une roche à Tintagel, Angleterre ©: Jeff Saward/Labyrinthos | Le labyrinthe du portique de la cathédrale de Lucques, Italie Merci à Wikipédia |
Dans la ville de Lucques en Toscane (Italie), la cathédrale a été construite à partir de 1063. Sur le portique d'entrée, on remarque un labyrinthe.
En Cornouaille (Angleterre), le site de Tintagel est célèbre car il passe pour avoir été le lieu de naissance et de résidence du roi Arthur. Dans une roche de la Rocky Valley, un labyrinthe a été sculpté, que certains datent de l'âge de bronze. Toutefois d'autres pensent qu'il date du 18e siècle de notre ère.
Il existe une abondance de labyrinthes dans le monde, sous des formes variées. Pour un parcours exhaustif des labyrinthes dans le monde voir le site Labyrinthos.
La spirale et le serpent ont été quelquefois façonnés dans le paysage, de telle sorte qu'on peut en ressentir l'énergie en marchant sur la terre. Ce sont aussi les vestiges d'un vaste complexe planétaire de régulation du réseau de flux vitaux de la terre, dans lequel les pyramides et les vortex sont omniprésents (voir article Alignements de sites sacrés).
Dans le vaste complexe de lignes tracées depuis des temps immémoriaux sur le sol désertique de la région de Nazca au Pérou, la spirale y figure en plusieurs endroits.
Le serpent est reproduit dans certains lieux sacrés antiques, par exemple Le Mont du Serpent (Serpent Mound) aux USA (Ohio). D'une longueur d'environ 400m, c'est un lieu traditionnel vénéré par les amérindiens. On pense qu'il a été édifié par le peuple Adena, qui vivait au début du premier millénaire.
 |  |  |
| Spirale de Nazca Photo Carmen Rohrbach, (Des messages dans le sable) Merci à Mystères et énigmes | Serpent Mound, Ohio, USA Merci à Wikipédia | Colline du Tor, Glastonbury, Angleterre |
La colline du Tor à Glastonbury est disposée en spirale. Elle est dédiée à Saint-Michel. Le caractère sacré donné au paysage par la spirale est dû à son évocation d'une force de croissance et d'élévation. Du lieu émanent des énergies électromagnétiques et gravitiques particulières, dues à sa position sur la ligne de courants cosmotelluriques appelée ligne St-Michel. Sur cette ligne qui traverse tout le sud de l'Angleterre, sont situés de nombreux sites religieux dédiés à St-Michel et à Marie (voir article Alignements de sites sacrés).
Nous terminons maintenant cette danse de spirales par une danse que nous effecturons nous-mêmes.
Certaines danses populaires reproduisent des spirales. C'est le cas de la danse bretonne An Dro. Les danseurs forment une chaine qui s'enroule lentement vers le centre. Puis elle repart vers l'extérieur, vers le monde manifesté.
Le corps et l'esprit participent pleinement. Si la danse se prolonge suffisamment longtemps, l'énergie dégagée par le groupe qui avance sur un rythme lent peut être très puissante. Parfois on est dans un état second.
d'après les travaux de Viktor Schauberger
Vidéo d'auteur inconnu - Durée 13 mn
La production d'énergie actuelle, que ce soit pour alimenter des installations industrielles, domestiques, ou des moyens de transport, est fondée sur une technologie de la dégradation. Ainsi, le moteur à explosion omniprésent fonctionne par l'explosion et la dégradation d'un mélange de gaz et d'essence. Le procédé engendre beaucoup de bruit et de chaleur, à la fois inutiles et nocifs pour l'environnement et les êtres vivants. Le rendement énergétique est médiocre.
Ce que nous faisons est erroné et contraire à la Nature car elle se meut autrement. Elle utilise principalement les énergies d'aspiration (c.a.d de succion) car elles lui sont indispensables pour développer et entretenir la vie. Elle ne fait appel aux énergies de pression et aux forces explosives que pour diminuer la qualité et pour la destruction. V. Schauberger (revue Implosion, 51, cité dans Le Génie de Viktor Schauberger, A. Bartholomew)
Schauberger s'est rendu compte de la puissance des vortex en observant comment les truites remontent les cascades par la force des vortex qu'elles créent dans le courant, grâce à leurs ouïes. Le vortex engendrent un mouvement tourbillonnaire dirigé de l'extérieur vers l'intérieur (force d'implosion) avec une vitesse croissante, qui condense et refroidit.
Schauberger a conçu des appareils divers basés sur ce concept d'implosion. Ils n'émettent pas de déchets et ne polluent pas. Il inventa maints générateurs qui fournissaient une puissance de sortie largement supérieure à celle qu'ils absorbaient (puissance d'entrée). Citons, parmi eux, des moyens de propulsions pour avions, sous-marins et voitures, différents appareils destinés aux habitations, produisant de l'énergie, du froid ou de la chaleur, et d'autres, remarquables, qui transforment une eau polluée en eau de source de haute qualité. Hélas, les prototypes en état de marche furent détruits à la fin de la seconde guerre mondiale et on ne dispose pas de leurs plans détaillés. Au cours de toutes ces expérimentations, il se rendit compte que la température et la structure de l’eau étaient critiques de même que la forme de sa turbine, ainsi que les matériaux utilisés pour sa construction. (A. Bartholomew)
Schauberger a inventé des turbines qui produisaient de l’énergie gratuite en faisant tourbillonner de l’eau glacée en la dirigeant vers le centre (turbine-truite). D'autres turbines employaient l'air. Une autre est conçue pour produire une force de lévitation sur une soucoupe volante.
L'information précise est difficile à obtenir, parce que Schauberger a été contraint de travailler pour les nazis sur les disques volants dans le secret. Tous les prototypes réalisés ont été détruits à la fin de la guerre. Toute l'information restante a été confisquée par les alliés russes et américains, puis par le consortium américain Donner-Gerchsheimer qui voulait exploiter son savoir en 1958 (date de sa mort).
 | 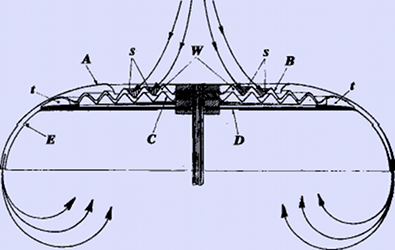 |
| Soucoupe volante de Schauberger. Diamètre 65 cm Extrait de Callum Coats cité par Disc Aircraft | Au centre, centripulseur en rotation rapide qui s'autoalimente sauf au lancement. On le lance avec un moteur; A: capot percé d'un trou au centre et de fentes s; l'air est aspiré par ces fentes, passe en W entre les membranes ondulées B et C où la force centrifuge le liquéfie, provoquant une force d'aspiration d'air supplémentaire, un semi-vide en-dessus de la soucoupe et une surpression en-dessous. Merci à Callum Coats |
Les hélices de bateau ont-elles un rapport avec les hélices définies en début d'article? Oui.
Ces hélices sont constituées de plusieurs pales dont chacune a la forme d'une portion d'hélice. C'est une hélice à plusieurs branches, en quelque sorte. Parce que la rotation entraine une progression de l'hélice, elle sert à propulser les bateaux et les avions. En tournant, les pales avancent dans l'eau en entrainant le bateau, ou dans l'air en entrainant l'avion. C'est l'inclinaison des pales qui détermine la valeur du pas de l'hélice.
Si l'hélice est fixée sur un bâti fixe, elle ne peut pas avancer, et elle fait circuler l'eau ou l'air. C'est le cas d'un ventilateur. Si l'hélice est placée dans un conduit, la circulation d'air est canalisée et se fait bien plus forte. Dans un conduit d'aération, l'air est aspiré puis envoyé vers l'arrière.
 |  |  |
| Hélice de bateau Merci à France-Hélices ™ | Ventilateur industriel Merci à Euroventilari | Avion à aile-gouttière CCW-5 de W. Custer Merci à Prototypes |
Ce dispositif a été utilisé par un inventeur étasunien méconnu, Willard Custer (1899 - 1985) pour concevoir des ailes d'avion plus efficaces, où l'air est canalisé dans une gouttière ou demi-tunnel. L'aspiration créée par l'hélice dans ce tunnel est suffisamment importante pour soulever l'avion sur une distance extraordinairement courte (30 m sur certains modèles). En 1929, après avoir expérimenté le principe sur une maquette volante, il dépose son brevet d'aile-gouttière ("Tunnel" ou "Channel Wing"), puis de nombreux autres. Mais l'histoire de ce créateur ressemble à celle de tout inventeur qui propose des solutions simples et économiques au service de l'humanité, qui vont à l'encontre des gigantesques projets commerciaux des grandes firmes. Il a été dénigré et rejeté.
Les éoliennes utilisent le même type d'hélice, mais selon le processus inverse. Lorsqu'on fait tourner l'hélice de propulsion au moyen d'un moteur, elle met en mouvement un courant d'air ou d'eau. Lorsque c'est le mouvement de l'air qui fait tourner l'hélice en entrainant un générateur électrique ou une pompe, c'est une éolienne.
 |  |
| Éolienne à axe horizontal Merci à Jonathan, Paul, Florian et Adrien | Éolienne à axe vertical windsite installée à La Ciotat Elle est silencieuse et ne tue pas les oiseaux Merci à BmyKey |
Lorsque les plantes croissent, la disposition de leurs feuilles, de leurs fleurs ou de leurs épines se présente géométriquement de deux façons. Soit elles sont disposées par groupe de 2 l'une en face de l'autre, soit elles naissent l'une après l'autre et elles se disposent en spirale. C'est le cas de la fleur de tournesol, de la pomme de pin, ou de la tige de céleri.
La spirale se forme à cause du mode de croissance de chacune des feuilles, fleurs ou épines. Prenons l'exemple de la tige de céleri. Au cours du processus de croissance, des ébauches de feuilles, composées de cellules encore indifférenciées, se développent les unes après les autres sur une proéminence conique en haut de la tige. Lorsqu'un nouveau pétiole (tige des feuilles) nait sur cette pointe, il se trouve dans l'espace laissé libre par les deux précédents (par exemple, la feuille 3 se place entre la 1 et la 2). Les pousses plus anciennes grossissent tout en s'éloignant du centre à une vitesse qu'on peut considérer approximativement comme continue et constante. La structure qui en résulte comporte plusieurs spirales qui tournent soit dans le sens dextrogyre, soit dans le sens lévogyre.
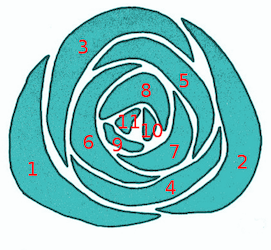
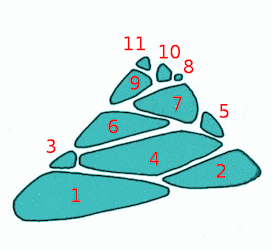
D'après Formes dans la Nature, P. Stevens
Ce qui est surprenant, c’est que l’arrangement des spirales est directement lié à la suite de Fibonacci et au nombre d’or. Si on compte les spirales dans une fleur de tournesol, on dénombre 21 spirales dans un sens et 34 dans l'autre. Dans une autre fleur de tournesol, 34 et 55, ou encore 55 et 89 ou 89 et 144. Dans l'ananas, on trouvera 8 rangs de fleurons dans un sens et 13 dans l'autre. Pour la pomme de pin, 8 rangs d'écailles dans un sens et 13 dans l'autre ou encore 2/3, 3/5, 5/8 ou 8/13. Pour la marguerite 21/34 et pour le céleri, 1/2.
Or tous ces nombres font exactement partie de la suite de nombres étudiée par la mathématicien Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 …On peut aborder le nombre dit nombre d'or par plusieurs voies. L'une d'elle est la symétrie 5 et la géométrie du pentagone (voir Géométrie cristalline). Une autre est la recherche de la meilleure façon de diviser un segment dans une proportion telle qu'on peut la poursuivre indéfiniment sur les segments obtenus. Précisément, je pars d'un segment AB que je veux diviser en 2 segments de façon harmonieuse, AC et CB.
Pour continuer la segmentation, je veux que la proportion entre AC et CB soit la même que celle entre AB et AC.
Autrement dit AC/AB = CB/AC = q
AC devient la nouvelle longueur à partager, entre AD et DC.
Ce qu'on nomme le nombre d'or φ est l'inverse de q: φ=1/q
Développement mathématique: Si je pose que AB = 1, alors AC = q et CB = q2.
Maintenant, je partage AC en deux segments AD et DC avec la même proportion. Alors, AD=q2 et DC=q3
On peut aussi bien procéder dans l'autre sens, partir d'un petit segment comme AC et calculer la longueur du segment supérieur AB dans la suite. C'est AB = AC/q. On multiplie par 1/q=φ
Calculons la valeur de q ou φ
AC + CB = AB, donc q2 + q =1 ou q2 + q - 1 = 0
La solution positive de cette équation est q= (-1+√5)/2 = 0,618...
Raisonnons avec φ: 1/φ2 + 1/φ -1 = 0 ou φ2 - φ - 1 =0
On en tire cette relation entre φ et 1/φ: φ = 1/φ +1 =(1+√5)/2 =1,618...
Le nombre d'or est devenu célèbre après qu'un moine italien, Luca Pacioli, ait fait paraitre en 1509 un livre La divine proportion dans lequel il dit que le nombre d'or possède les attributs trinitaires de la Divinité.
Auparavant, on connaissait la suite de Fibonacci depuis le début du 13e siècle. Le mathématicien Léonard de Pise, dit Fibonacci (le fils de Bonacci), avait étudié la série de nombres qui porte son nom, citée plus haut. Elle est construite à partir du chiffre 1 avec la règle que chaque terme de la suite est la somme des deux précédents.
Or si on divise un terme par le précédent ou le suivant, on a une valeur proche du nombre d'or, d'autant plus proche que les nombres sont plus élevés. Dès les premiers termes 2 et 3, on s'en approche 3/2=1,5 ou 2/3= 0,66. C'est la proportion des 2/3. On va rapidement vers 0,618 avec 55/34=1,6176
Lorsque les pétioles apparaissent un à un, ils forment un angle précis avec le pétiole précédent et le centre, toujours à peu près le même. Cet angle résulte d'une occupation optimale de l'espace laissé par les pétioles précédents. Si ceux-ci ne bougeaient pas, la répartition équitable de 3 pétioles serait de 1/3 du cercle chacun, soit un angle d'écart de 120°. Or ils s'éloignent du centre. Cela a pour conséquence que l'angle du point 3 avec le point 2 est plus grand que celui avec le point 1. Il est de 137,5°.
Cet angle est celui qui permet une division du cercle de 360° en deux arcs selon la proportion du nombre d'or, et on le nomme l'angle d'or. Vérifions: 360° x 0,618 c'est 222,492° soit 222° 29' 32" pour l'angle rentrant. Son complément saillant est précisément 137° 30' 28".
Les plantes et certains coquillages croissent selon cet angle, démontrant ainsi que cet angle, et plus largement cette proportion, résultent naturellement de la structure de notre espace-temps. Toutefois, il ne faudrait pas en conclure qu'elle est le seul schéma géométrique sous-jacent de notre univers.
Si je marche le long de la ligne d'une spirale plane, tel une fourmi, en partant du centre et en allant vers l'autre extrémité, je m'écarte progressivement du centre. Si je trace un rayon du centre jusqu'à moi, la longueur R de ce rayon augmente au fur et à mesure que je me déplace vers l'extrémité extérieure. Si cette augmentation est régulière, on peut la formuler mathématiquement par la valeur de R. Le déplacement est repéré par l'angle parcouru depuis le départ (A). Cet angle, bien entendu, dépasse la valeur 360° dès que j'ai effectué mon déplacement sur la première spire.
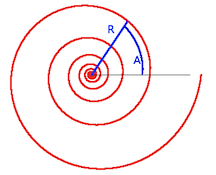 |  |  | |
| Spirale d'Archimède Merci à Robert Ferréol | Cliché A. Boudet © | Spirale de Fermat Merci à Robert Ferréol |
Lorsque je m'éloigne de la même distance à chaque tour, la distance est proportionnelle au nombre de tours et plus précisément au déplacement A. C'est le cas lorsque les spires sont jointives. On obtient la spirale d'Archimède R = k A .
Si la spirale s'éloigne d'abord rapidement, puis de moins en moins, on a la spirale de Fermat, R = k √ A
Si le rayon croit de façon exponentielle, R = k epA , alors c'est la spirale logarithmique dite de Bernoulli. Elle a la propriété remarquable que sa trajectoire fait toujours le même angle avec le rayon. Pour cette raison, elle est aussi nommé spirale équiangle.
 | 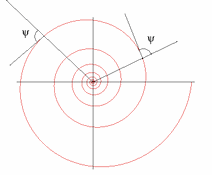 |  |  |
| Spirale logarithmique Merci à Robert Ferréol | Dans la spirale logarithmique, l'angle avec la tangente est constant Merci à Robert Ferréol | Spirale hyperbolique Merci à Robert Ferréol | Lituus Merci à Robert Ferréol |
Lorsqu'on s'éloigne de façon encore plus rapide, on a la spirale hyperbolique R = k /A
Dans le lituus, on a R = k /√A .
Le lituus est un baton étrusque utilisé dans la Rome antique. Il est l'ancêtre de la crosse des évêques et a donné le mot liturgie.

Il existe d'autres types de spirales dont le rayon ne croit pas de façon continue, mais par à-coups. Par exemple, avec un compas, on peut dessiner une spirale qui commence par un demi-cercle. Puis on recule la pointe centrale du compas et on continue avec un autre demi-cercle. On a donc maintenant 2 centres. Puis on recule au premier centre et on trace le troisième demi-cercle, et ainsi de suite. On a construit une spirale à 2 centres.
On peut de la même façon construire une spirale à 3 centres qui sont situés aux trois sommets d'un triangle équilatéral, et on trace des tiers de cercle; à 4 centres qui sont situés aux quatre sommets des angles d'un carré et on trace des quarts de cercle, etc.
 | 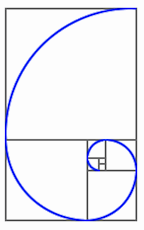 | 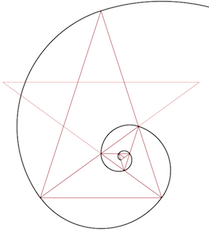 | 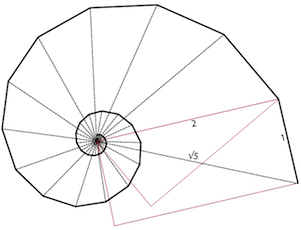 |
| Spirale d'arcs à 6 centres Merci à Gabriel Martinez | Principe de construction des spirales du rectangle d'or et de Fibonacci | Spirale du triangle d'or Merci à Gabriel Martinez | Spirale à segments Merci à Gabriel Martinez |
Une autre catégorie de spirales repose sur le principe du changement de centre à chaque tracé d'arc de cercle. On a autant de centres que d'arcs. C'est le cas de la spirale du rectangle d'or. On part d'un carré de côté 1 pour tracer le premier quart de cercle. Ensuite, on recule le centre afin d'avoir un rayon de longueur φ, le nombre d'or = (1 + √5)/2 = 1,618 et on trace le deuxième quart de cercle. Puis on recule le centre pour obtenir un rayon de longueur φ2 et on trace le troisième, etc. L'angle de la trajectoire avec le rayon est constant et égal à 73° ce qui montre que la spirale du rectangle d'or est proche d'une spirale logarithmique.
Si, au lieu de partir d'un rectangle d'or, on part d'un rectangle de Fibonacci, et que les longueurs successives des côtés des rectangles sont les nombres de la série de Fibonacci, on obtient une spirale de Fibonacci qui est très proche la spirale d'or, mais qui ne possède pas la propriété d'angle tangentiel constant.
Si on part de 3 centres en triangle isocèle, dont les 2 côtés égaux sont en rapport φ avec le troisième, c'est la spirale du triangle d'or.
Enfin, on peut tracer une spirale comme une suite de nombreux segments courts. En traçant les rayons qui joignent leurs extrémités, on définit une suite de triangles. On se donne une règle qui définit les longueurs du rayon et du côté de chaque triangle. Dans le tableau, voici une spirale qui est basée sur des triangles dont le côté est de longueur 1, et le rayon de longueur 2. Le troisième côté, de longueur √5 devient le rayon du triangle suivant.
Spirales dans la nature
Spirales dans l'Univers
Art et cultures
Labyrinthes et jeux initiatiques
Spirales en mathématiques
| | | |
| | | |
Texte conforme à la nouvelle orthographe française (1990)
04 janvier 2013