

Les notes de musique
doivent-elles être normalisées par un diapason
(LA 440, LA 432 ou autre)?
Les aléas historiques de la fréquence du LA
Première partie
Alain Boudet
Résumé: 1. Depuis 1953, une norme internationale recommande d'accorder les instruments de musique à la fréquence de 440 hertz pour le LA. C'est une volonté récente, car dans le passé, on ne s'intéressait qu'aux intervalles entre les notes et on ne savait pas mesurer leur fréquence.
2. Fixer un diapason à 1 Hz près a un sens purement technique car musicalement, les notes émises par les instruments sont fluctuantes et varient avec la température et le souffle. Lorsque vous entonnez une chanson, vous ne vous souciez pas du diapason. La nécessité d'un diapason commun est apparue pour des motifs pratiques et commerciaux, afin de faciliter la musique professionnelle d'ensemble et la fabrication des instruments.
3. Au moins jusqu'au 18e siècle, le diapason des instruments variait d'un endroit à l'autre, d'une époque à l'autre et d'un instrument à l'autre. Puis des tentatives de normalisation ont été effectuées, mais le choix des valeurs retenues a suscité des controverses, qui ne se sont pas éteintes avec la normalisation internationale de 1953.
4. Le choix d'un diapason plus haut ou plus bas peut affecter le rendu sonore et la performance vocale des chanteurs lorsqu'il s'agit d'interpréter des œuvres écrites dans le passé. L'essentiel est l'impact émotionnel et physique de la musique sur l'auditeur. Il résulte de paramètres complexes qui dépassent de loin la question du diapason.
Contenu de la première partie
Contenu de la troisième partie
Contenu de la quatrième partie
Dans mes articles sur la musique, nous avons constaté que l'identité d'un mode musical repose sur la valeur des intervalles entre les notes qui le constituent, autrement dit sur les rapports que les notes ont entre elles. Nous indiquons par exemple que deux notes sont distantes d'une tierce ou d'une quinte (voir Défilés de modes). Nous avons également précisé qu'il y avait plusieurs valeurs possibles de la grandeur de cette tierce ou de cette quinte, selon le système d'intonation choisi, gamme tempérée ou autre (voir Ton et intonation juste).
Cela dit, à aucun moment nous n'avons défini une hauteur pour une note seule, isolée, un LA ou un DO par exemple, sans la relier à une autre. Autrement dit, nous n'avons pas porté d'attention à la hauteur absolue des notes. Elle n'est pas intervenue dans les définitions et les choix des modes musicaux.
Cette absence de référence à une hauteur fixe était de mise dans la pratique musicale du passé jusqu'au 18e siècle, qui ne considérait que les intervalles entre les notes. Mais il est apparu récemment le besoin pratique de fixer la hauteur d'une note de référence, hauteur nommée le diapason, d'abord le DO puis le LA.
De nos jours, tout chœur, avant d'exécuter une œuvre, prend le ton, c'est-à-dire que le chef entonne la première note qui sera chantée par chacune des voix, en se référant au diapason admis. De même, les musiciens d'un orchestre règlent leurs instruments afin que leur LA ait la hauteur assignée.
Nous sommes tellement habitués à faire référence au diapason de fréquence 440 Hz, fréquence produite par l'objet métallique en forme de fourche nommé également diapason, ou par son homologue électronique, que nous ne nous demandons plus pourquoi et comment cette valeur a été déterminée. Il nous semble que cela fait partie des choses normales qu'on ne discute pas.
Or c'est faux. Le diapason, au contraire, a été beaucoup discuté au moment où il est apparu dans l'histoire et il se discute encore maintenant.
La normalisation du LA à 440 Hz est une recommandation internationale récente qui n'est pas obligatoire et n'est pas forcément respectée. C'est pourquoi, dans le monde, les fréquences du LA adoptées par les orchestres s'étalent sur une certaine plage. Elles sont souvent plus hautes que 440, par exemple 442 ou 444 Hz (voir le site de Franz Nistl, accordeur de piano).
En contraste avec cette normalisation, l'accordage des instruments anciens au cours des 15e à 19e siècles s'étalait sur une plage d'environ 3 tons.
Depuis deux siècles environ, certains musiciens ont milité, ou militent actuellement, en faveur d'une valeur bien particulière du diapason. Les uns réclament un LA de 432 Hz, d'autres un DO de 256 Hz, d'autres un MI de 528 Hz, etc., chacun estimant qu'il prône la meilleure valeur pour des raisons très éclectiques, parfois étayées, parfois circonstanciées, parfois étranges ou imaginaires.
Cette situation nous amène à nous poser quelques questions:
C'est ce que j'explore dans les 4 parties de cet article. Je ne donne pas de réponse définitive sur le choix d'une valeur ou d'une autre. Je montre essentiellement la réalité de la pratique musicale et son rapport avec les aspirations des êtres humains. Le reste est affaire de gout personnel et de circonstances.
La hauteur de la note choisie comme référence (actuellement LA, anciennement DO ou FA) est appelée le diapason (en anglais concert pitch, en allemand Kammerton).
Ce sens récent dérive de sens anciens bien différents. Dans son Encyclopédie, Denis Diderot (écrivain et philosophe français, 1713 - 1784) relate en 1780:
DIAPASON: Intervalle de l'octave selon les anciens.
Il ajoute deux autres sens qui ne se réfèrent pas du tout à une hauteur fixe:
Tables dont se servent les facteurs d'instruments de musique.
Étendue des sons convenable à une voix ou à un instrument.
Pour disposer d'un repère pour cette "étendue convenable", les chanteurs et instrumentistes se sont servi d'instruments qui font entendre une note témoin et qui ont été nommés diapason.

L'instrument - que j’appellerai diapason-fourche - est constitué d'une fourche en métal qui vibre et émet ce son lorsqu'on la frappe. La hauteur du son peut être ajustée en modifiant la hauteur des branches. Son invention est attribuée au trompettiste et luthiste anglais John Shore (1662-1752) en 1711. Le son émis est faible et pour mieux l'entendre, on doit poser l'instrument sur un résonateur, par exemple un petit caisson en bois, ou tout simplement sur le dessus d'un meuble.
Par dérivation, [la note témoin] étant habituellement le LA 3, on en est venu à parler du « la du diapason », puis de « diapason » tout court. (Jacques Chailley, Encyclopédia Universalis)
Ces instruments mécaniques sont de plus en plus remplacés par des appareils électroniques et d'excellentes "applis" pour téléphones mobiles qui produisent les fréquences sonores désirées.
Le mot diapason est également employé pour les instruments à corde comme le violon ou la guitare pour désigner la longueur de la partie vibrante de la corde à vide. Ainsi pour le violon, le diapason est la longueur depuis le chevalet de la table jusqu'au sillet de la tête de manche, qu'on divise en deux parties, du chevalet jusqu'au rebord de la table et de ce rebord jusqu'au sillet.
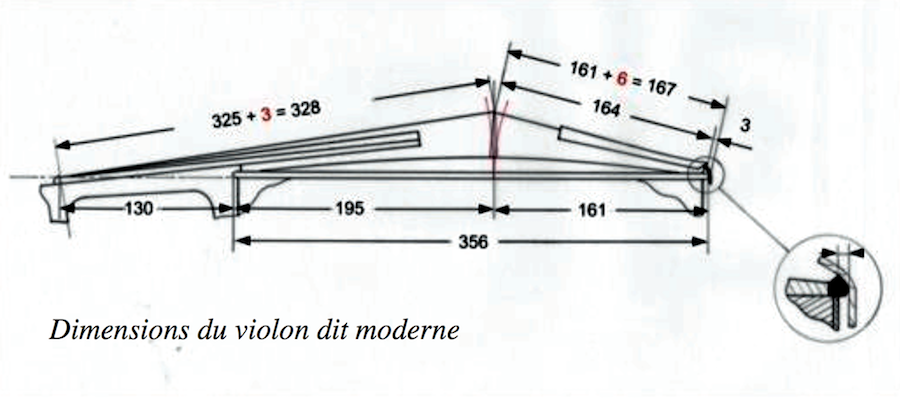
Dessin de Christian Urbita, luthier à Cordes sur Ciel.
Reproduit de: Quelle longueur de corde vibrante pour le violon d’aujourd’hui ?
Puisque la hauteur de la note LA est fixée par sa fréquence, il serait bon de s'interroger sur le sens musical de ce mot. Parler de la fréquence d'un son musical semble banal, mais c'est historiquement très récent. Cette notion a été introduite par les physiciens, plus exactement les acousticiens, à partir du 17e siècle. Elle s'est répandue plus tard chez les musiciens par l'usage d'instruments de mesure modernes, surtout électroniques. (Pour plus de détails, voir l'article: Histoire de la notion de fréquence sonore)
Traditionnellement, en musique, on ne parlait pas de la hauteur absolue d'un seul son, mais de la différence de hauteur entre deux sons (hauteur relative), autrement dit de la grandeur des intervalles entre sons.
On exprime la grandeur de ces intervalles en tons et en demi-tons, ou encore en comma, qui vaut environ 1/9e de ton ou 22 cents. Le cent est par définition 1/100e de demi-ton (un demi-ton = 100 cents), et il y a 1200 cents dans une octave (voir article Sons: hauteur et fréquence).
Lorsqu'on a été capable de mesurer des fréquences, on a déterminé que le demi-ton, dans le système de tempérament égal, équivaut à un rapport de fréquences de 1,0595 et que le ton équivaut à un rapport de 1,1225.
Puisqu'on ne savait pas mesurer des fréquences, comment les musiciens déterminaient-ils la valeur des intervalles entre les notes? Par exemple comment le philosophe grec Pythagore (vers 580 - vers 495 av.J.C.) pouvait-il définir les quintes, les tons et le comma?
Pythagore étudiait les sons musicaux à l'aide d'un instrument qu'il avait construit. Dans un ouvrage de 1706 intitulé La Vie de Pythagore, ses symboles, ses vers dorez et la vie d’Hiéroclès, André Dacier écrivait: [Pythagore] fit un instrument de la muraille de la chambre, avec des pieux qui tenaient lieu de chevilles et des cordes d'égale longueur, au bout desquelles il attacha différents poids, et en frappant plusieurs de ces cordes ensemble, il en formait différents accords et s'instruisait par là des raisons de cette différente harmonie, et des intervalles qui la causaient; et pour cela il fit le célèbre canon d'une seule corde, qui fut appelée le canon de Pythagore, où il marqua toutes les proportions harmoniques. (kanon en grec = la loi, la règle)
Le canon est aussi appelé monocorde. C'est en mesurant la longueur de la partie vibrante de la corde qu'on pouvait déterminer des intervalles avec précision.
Au Moyen-Âge et à la Renaissance, on étudiait les sons avec un monocorde, variante de celui de Pythagore. Boèce, philosophe et homme politique romain (vers 480 - 524), dans son traité De institutione musica, transmit de nombreux éléments théoriques et pratiques sur son utilisation.
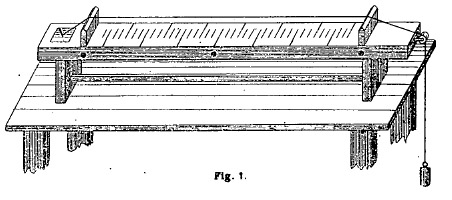
Un exemple de monocorde
Extrait de: La musique et les musiciens,
Albert Lavignac, 1938, p.7
édition numérique Gallica
Merci à Metronimo
Guido d'Arezzo, moine bénédictin italien (992 - apr. 1033) en étendit l'usage et trouva des procédures plus simples pour déterminer les intervalles, qu'il décrivit dans son traité Micrologus de disciplina artis musicæ.
Selon Denis Diderot dans son Encyclopédie de 1765, Le monocorde ancien était composé d'une règle divisée et subdivisée en plusieurs parties sur laquelle il y avait une corde de boyau ou de métal médiocrement tendue sur deux chevalets par les extrémités; au milieu de ces deux chevalets, il y en avait un autre mobile par le moyen duquel, en l'appliquant aux différentes divisions de la ligne, on trouvait en quel rapport les tons étaient avec les longueurs des cordes qui le rendaient. [...]
Lorsque la corde est divisée en deux parties égales, de façon que les parties soient comme 1 à 1, on les appelle unisson; si elles sont comme 2 à 1, on les nomme octave ou diapason; comme 1 à 3 quinte ou diapente; comme 4 à 3, quarte ou diatesseron; comme 5 à 4, diton ou tierce majeure; comme 6 à 5, demi-diton ou tierce mineure; enfin comme 14 à 25, demi-diton ou dièse.
Dans le monocorde, la hauteur du son émis par la corde entière en vibration n'est pas fixe. Elle dépend de plusieurs paramètres.
La hauteur du son de la corde libre dépend de la longueur entre les deux chevalets extrêmes (longueur de corde vibrante). Plus courte est la corde, plus haut est le son.
La hauteur dépend aussi de la grosseur de la corde. Dans les instruments où l'on a plusieurs cordes, la grosseur peut varier d'une corde à l'autre et la comparaison des sons ne peut être faite que par les longueurs mesurées sur une même corde.
Enfin, la hauteur dépend de la tension de la corde. La corde du monocorde est tendue au moyen d'un poids de valeur donnée. La tension change d'un jour à l'autre ou d'un moment à l'autre en fonction des fluctuations des caractéristiques physiques de la corde sous l'effet de la température et de l'humidité. Le son produit change donc pareillement.
La corde ne fournit donc pas de son fixe de référence.
Dans leurs expérimentations, ces érudits inséraient un chevalet mobile pour partager la corde en fractions simples. La position du chevalet mobile était repérée sur une règle graduée au moyen de lettres (qui deviendront bien plus tard les noms des clés), et on comparait le son émis par les deux fractions de corde en fonction du rapport de leurs longueurs.
Comme le dit Diderot, diviser la corde en 3 parties en plaçant le chevalet au 1/3 ou 2/3 de sa longueur produit la quinte. La diviser en 5 produit la tierce. La tierce n'était pas prise en considération par Pythagore qui n'utilisait que les quintes et le rapport 2/3 dans l'élaboration de ses modes. La tierce juste avec son rapport 4/5 sera introduite dans la gamme par Gioseffo Zarlino, compositeur italien de la Renaissance (1517-1590) (voir article Ton et intonation juste).
Dans toutes les études rapportées depuis Pythagore jusqu'à la Renaissance, il n'est nullement question de sons fixes de référence. On ne mentionne que des rapports de longueur de corde. La hauteur de la corde à vide était fluctuante selon le moment. La notion de hauteur absolue était étrangère à la mentalité des musiciens. La notion de fréquence n'existait pas encore.
Les études scientifiques du 19e siècle ont démontré et précisé les caractéristiques vibratoires du son. La découverte de l'électricité a suscité l'invention d'appareils d'enregistrement et de mesure (microphone, oscilloscope...) qui affichent et donnent toutes les caractéristiques physiques du son.
Les notions d'ondes sonores, de fréquences et d'harmoniques ont été diffusées par les physiciens. Elles font maintenant partie de notre enseignement scolaire et de notre culture commune. Actuellement, n'importe quel ordinateur domestique ou smartphone peuvent enregistrer des sons et les analyser, avec un logiciel adéquat. (Pour plus de détails, voir l'article: Histoire de la notion de fréquence sonore)
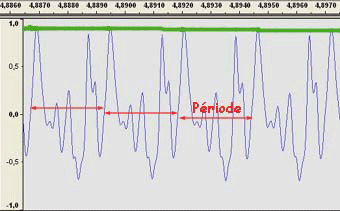 |  |
| Courbe
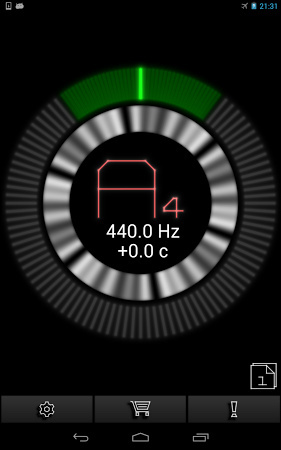
de variation de la pression d'une onde sonore à l'échelle des millièmes de seconde. Elle montre sa répétition périodique (fréquence). Réalisé avec le logiciel Audacity | Écran d'un téléphone portable avec l'application "PitchLab Instrument tuner" affichant la fréquence d'un son et la note correspondante |
Les musiciens ont donc pris l'habitude d'exprimer la hauteur des sons en fréquence pour accorder leurs instruments. Ils utilisent pour cela des diapasons électroniques qui sont mis à leur disposition. Les musiciens peuvent ainsi régler la fréquence de leur LA avec une grande précision.
Toutefois, cette pratique d'accord de fréquence au diapason international issue de l'appareillage disponible ne doit pas nous dispenser de nous interroger sur son sens et son intérêt musical.
Mesurer la fréquence des sons avec une précision de 0,1 Hz signifie-t-il pour autant que cela soit nécessaire ou utile dans la pratique musicale? Et que l'esthétique musicale en tire avantage? La suite de cette étude va nous permettre de nous rendre compte que tout est affaire de circonstances.
Texte conforme à la nouvelle orthographe française (1990)
8 aout 2016 - modification 31 aout 2017