

Cristaux et Géométrie cristalline
Alain Boudet
Dr en Sciences Physiques
Résumé: Un cours pour débutants sur la géométrie cristalline. Le diamant et le quartz sont des cristaux typiques par leur transparence pure et leurs formes géométriques. La géométrie extérieure est la manifestation d'une géométrie intérieure. Les cristaux sont construits par l'empilement ordonné périodique de petites briques atomiques élémentaires, les mailles. Lorsque cet ordre fait défaut, la matière est dite amorphe ou vitreuse. La cristallisation est une transformation extraordinaire qui fait passer du désordre liquide à l'ordre compact. Les roches, et toute matière y compris les matériaux industriels (métaux, silicium, polymères), contiennent des domaines cristallins et amorphes. Récemment on a reconnu l'existence de domaines cristallins aux géométries plus complexes (les quasi-cristaux), dont la périodicité n'est détectable que dans un espace à dimension supérieure. Les cristaux fournissent des exemples de la façon dont l'espace peut être pavé par des polyèdres tels que cube, octaèdre, dodécaèdre. Cet article vise à révéler la beauté, la précision et l'intelligence des formes géométriques cristallines.
Vous voulez en savoir plus sur les cristaux, mais vous en avez déjà une idée. Alors, à votre avis, qu'est-ce qu'un cristal? Au fond, le savez-vous? Que répondriez-vous à un enfant qui vous le demande?
Ce mot vous fait-il penser à la vaisselle de luxe de grand-mère, aux magnifiques minéraux de la terre, ou encore à une construction atomique géométrique? La notion de cristal renvoie à différents sens.
Le but de cet article est donc de brosser un panorama des caractéristiques des cristaux dans leurs différents aspects. Mais ce panorama n'a de sens que parce qu'il invite à révéler la beauté, la précision et l'intelligence des constructions cristallines. Nous constaterons aussi que les cristaux sont omniprésents comme matière ou éléments technologiques dans notre environnement, souvent inaperçus.
Votre premier contact avec les cristaux a peut-être été d'admirer la vitrine d'un marchand de cristaux, de les observer et de les toucher. Il vend des minéraux, des gemmes, des pierres précieuses et des cristaux, 4 noms qui désignent des objets proches mais pas tout-à-fait identiques.

Wulfénite (Ojuela Mine, Mapimi, Durango, Mexique) en association avec de la mimétite verte
Photo Frédéric Hède ©Alpinisme et minéraux
Le terme minéral décrit un élément de l'écorce terrestre. Les êtres existant sur cette terre sont classées en 3 règnes dont l'un est le minéral, les 2 autres étant le végétal et l'animal. Donc, ce qui n'est ni végétal, ni animal est minéral. Toutefois, pour être précis et ne pas enfermer l'esprit dans des idées rigides, il faut noter que certains organismes microscopiques sont à la frontière entre deux règnes (minéral/végétal ou végétal/animal) et peuvent être classés soit dans l'un soit dans l'autre selon le critère retenu pour définir un règne (mobilité, capacité à respirer, etc.). Comme pour toute classification décidée par l'esprit, il n'y a pas de critère unique et définitif.
Selon leur composition et leur histoire géologique, les minéraux sont plus ou moins durs (de l'argile pâteuse au silex et au diamant), plus ou moins compacts, friables ou fragmentés (comme le sable). Le mot pierre désigne un minéral plutôt solide et compact. Certaines de ces pierres sont qualifiées de gemmes, de pierres précieuses ou de pierres ornementales.
Les pierres précieuses sont précieuses à cause de leur beauté, de leur rareté et de leur valeur commerciale. Elles sont principalement transparentes et sont au nombre de 4: le diamant, le rubis, le saphir et l'émeraude.
Les pierres fines sont translucides ou transparentes. On peut citer la topaze, le quartz, l'opale, les grenats, l'aigue-marine, la tourmaline, l'améthyste et bien d'autres encore.
Le terme pierre ornementale s'applique à toutes les pierres qui sont portées comme parure. Il est souvent employé comme synonyme de pierre fine. Les pierres ornementales sont translucides ou opaques. On peut citer l'obsidienne, la moldavite, etc.
Le mot gemme englobe les pierres précieuses, fines ou ornementales. Une pierre gemme doit posséder les trois caractéristiques suivantes: avoir un aspect agréable, principalement par sa couleur, avoir une dureté élevée (pour éviter d'être abimée par les frottements et rayures) et être rare. La pierre doit aussi être peu altérable sur le plan chimique. (plus de détails dans le site Kasaku)
Cristaux géants de gypse (sulfate de calcium) dans une grotte de Naica au Mexique.
Vous pouvez aussi consulter cette vidéo.
Dans l'usage courant, il n'y a pas de frontières précises entre ces différentes catégories. Toutefois, des règles commerciales ont fixé la dénomination de pierres précieuses afin que l'acheteur soit bien informé de ce qu'il achète. La notion d'ornement est subjective et divers objets de matière dure ou colorée ayant l'aspect de pierreries peuvent être nommés pierres ornementales. Des substances d'origine organique telles que le corail, l'ambre, les perles sont assimilées aux gemmes.
Enfin, le terme cristal inclut la plupart des pierres gemmes. Dans le domaine de la joaillerie, il est difficile de préciser les limites de son emploi et les différences par rapport à celui de gemme. Toutefois, le terme fait plutôt référence à la forme extérieure géométrique et régulière de ces pierres. Les scientifiques ont retenu cette caractéristique, transposée sur le plan atomique, pour donner leur propre définition du cristal.
Les pierres fines et précieuses ne tirent pas seulement leur valeur de leur beauté. Beaucoup possèdent des vertus curatives et protectrices qui ont été reconnues de tout temps dans de nombreux pays. En portant ces pierres sur soi, ou en les disposant dans une maison, on ajoute leur action curative à leur effet esthétique et décoratif, à condition de savoir en prendre soin. De nombreux sites donnent des renseignements à ce sujet (exemple: Énergies et cristaux).
Leur effet curatif et protecteur n'a pas été scientifiquement expliqué. Deux types de mécanismes sont à l'œuvre dans les cristaux. D'une part ils émettent des rayonnements. Ceux-ci sont en rapport avec la couleur du cristal, mais la couleur n'explique pas tout. D'autre part ils emmagasinent des énergies issues de leur environnement dans leurs structures internes, ils les enregistrent en quelque sorte. Il est fort possible que cette mémorisation se produise à des niveaux sous-atomiques (voir Codes, information et enregistrement).
Dans le domaine des pierres ornementales, le terme cristal est fréquemment associé à celles qui sont transparentes. D'un usage encore plus restrictif, il désigne parfois le cristal de roche, autre nom du quartz qui frappe par sa transparence d'une grande limpidité (voir en annexe Quartz).
L'étymologie peut nous éclairer. Le terme cristal est dérivé du grec krystallos qui signifie la glace. A l'origine le mot veut signifier que la roche est transparente et compacte comme la glace.

Par extension, le mot cristal désigne ce qui est limpide comme l'eau pure. On parle d'eau cristalline (Dans le cristal d'une fontaine, Un cerf se mirant autrefois... Jean de La Fontaine), et de voix cristalline.
Le papier cristal est un papier transparent du commerce, utilisé par exemple par les fleuristes pour emballer les bouquets.
Le verre de cristal utilisé pour la vaisselle de luxe n'est ni du cristal de roche, ni ne présente aucune structure géométrique. Sa structure est amorphe (ou vitreuse, c'est-à-dire désordonnée - voir plus loin). Son appellation cristal se justifie par la pureté de sa transparence, due à sa composition chimique riche en oxyde de plomb. Les magasins de cristallerie vendent de la verrerie, mais ce ne sont pas des gemmes !!!
Dans son emploi relatif aux verres de cristal, au papier cristal et à l'eau cristalline, le mot cristal est en désaccord avec son autre usage en rapport avec la structure géométrique telle que nous allons la définir ci-dessous. En effet, la structure de l'eau et celle du papier cristal sont amorphes comme celle du verre, et non cristallines. Toutefois, désaccord ne signifie pas que l'une est fausse et que l'autre doit s'imposer. Cela signifie, comme il arrive souvent dans le dictionnaire, qu'un même mot peut avoir plusieurs sens selon les communautés qui l'emploient.
Le terme cristal évoque un minéral aux formes géométriques régulières. En effet, l'observation de gemmes (calcite, quartz) montre que beaucoup de ces cristaux sont délimités par des facettes planes régulières qui se coupent à angles vifs selon des symétries flagrantes. Elles laissent apparaitre des cubes, des pyramides ou des prismes, ou des volumes plus complexes à faces planes appelés polyèdres (nous en verrons des exemples).
De telles géométries existent aussi dans des cristaux autres que les gemmes. Si l'on dissout en quantité suffisante du gros sel de cuisine (chlorure de sodium) dans de l'eau, puis qu'on laisse cette eau s'évaporer lentement, il reste des cristaux de sel de forme cubique (fig.1). On trouve aussi de telles géométries régulières dans les cristaux de glace qui se forment lorsque l'eau gèle.
Cette surprenante régularité des formes a incité des scientifiques à les examiner minutieusement à l'œil nu et à la loupe, afin d'en déterminer les règles, bien avant que la notion d'atome soit reconnue et acceptée. C'est l'origine de la cristallographie. Afin de comprendre ces règles, nous allons suivre ces savants dans leurs recherches pour établir les lois de symétrie et l'existence d'un volume élémentaire dès le 17e siècle.
Notons toutefois que ces formes régulières visibles à l'oeil nu ne sont pas systématiquement présentes dans les cristaux. La forme des gemmes est extrêmement variable, elle reflète l'histoire de la pierre, la façon dont elle s'est formée, les conditions de température, d'humidité et de pression et le temps de croissance dans le terrain où elle est située, l'érosion à laquelle elle a été soumise. Celles qui présentent une forme régulière bien développée nous émerveillent et retiennent notre attention. Quant aux autres, elles présentent également un caractère cristallin qui ne peut être établi qu'au microscope (voir plus loin les matériaux polycristallins).
Au 17e siècle, plusieurs savants pressentent que les faces cristallines font entre elles des angles déterminés et constants. Dans la deuxième moitié du 18e siècle, Jean-Baptiste Louis Romé de L'Isle le vérifie et le démontre avec l'aide de ses collaborateurs. Ils fabriquent des modèles de cristaux en terre cuite, en carton ou en cuivre, puis mesurent les angles de façon plus précise à l'aide d'un rapporteur.
A la fin du 18e siècle, l'abbé René Just Haüy s'intéresse aux formes polyédriques des cristaux. Il avait fait tomber sans le vouloir un cristal de calcite qui s'est brisé. Examinant les fragments, il constata qu'ils n'étaient pas informes comme des morceaux de verre brisés. On y voyait toujours le même type de facettes, semblables à celles du morceau d'origine, quelle que soit leur taille. En brisant à nouveau ces morceaux de calcite, on crée des morceaux plus petits sur lesquels on retrouve la même forme régulière, sorte de parallélépipède déformé en losange (nommé aussi rhomboèdre).
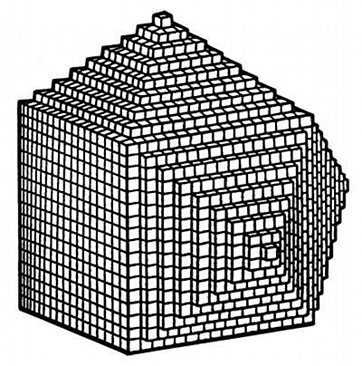
Fig.2- Dessin de Haüy extrait de son ouvrage Essai d'une théorie de la structure des cristaux, 1784
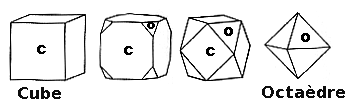
Fig.3- Les formes tronquées du cube
Fig.4- Octaèdre régulier obtenue en tronquant les sommets du cube.
© A. Boudet
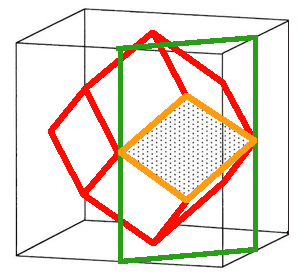
Fig.5- Dodécaèdre rhombique obtenu en tronquant les arêtes du cube.
© A. Boudet
Haüy imagine que la division en morceaux de plus en plus petits doit avoir une limite, une unité insécable, un volume élémentaire, trop petit pour être isolé par nos instruments. Dans le cas de la calcite, ce volume a la forme d'un rhomboèdre. En 1840 son élève, Gabriel Delafosse, nomme ce volume la maille élémentaire. Ces volumes élémentaires s'empilent parfaitement les uns sur les autres comme des briques pour reconstituer les cristaux naturels (fig.2).
Haüy rechercha les mailles élémentaires de nombreux types de cristaux et découvrit qu'elles se réduisaient à un petit nombre de formes: dodécaèdres, prismes hexagonaux, octaèdres et tétraèdres. Ce n'est qu'avec l'avènement de la théorie atomique et les mesures aux rayons X que ces notions seront complétées et précisées.
Dans cette recherche d'une définition géométrique du cristal, nous arrivons à la conclusion que la structure d'un cristal est la répétition d'une maille élémentaire dans les trois directions de l'espace.
Comment expliquer que les facettes des cristaux ne restent pas plates et présentent des formes irrégulières, des marches, des terrasses, des pyramides, etc.? Dans son Essai d'une théorie de la structure des cristaux, l'abbé René Just Haüy avance une explication ingénieuse. Une face est plane lorsque les mailles élémentaires sont accolées les unes contre les autres à la surface et toutes présentes, comme un pavage uniforme.
Mais en ajoutant ces mailles de façon régulière en dégradé à partir des arêtes, comme des excroissances, on obtient des escaliers à marches régulières qui forment des pentes à inclinaisons bien définies qui créent des formes telles que des pyramides (fig.2 - voir plus loin Formation des cristaux).
Bien que ces formes pyramidales se soient créées en tant qu'excroissances, on peut les voir géométriquement comme des formes tronquées.
À partir d'un volume en forme de cube, si on le tronque par un plan incliné qui unit les sommets opposés (en vert sur la figure 4), et qu'on le fait dans les 3 orientations, on obtient un polyèdre à 8 faces triangulaires (en rouge). Un polyèdre à 8 faces est nommé octaèdre. Il existe de nombreux octaèdres qui différent par la forme de leurs faces. Dans l'octaèdre régulier, les 8 faces sont des triangles équilatéraux (leurs 3 côtés sont de longueur égale).
Si on tronque le cube parallèlement au plan qui unit deux arrêtes opposées (en vert sur la figure 5), et qu'on le refait dans les 6 orientations, on obtient un polyèdre de 12 faces losangiques (en rouge). Un polyèdre à 12 faces est nommé dodécaèdre. Il existe de nombreux dodécaèdres qui différent par la forme de leurs faces. Nous avons obtenu un dodécaèdre losangique, mais comme dans ce domaine on emploie les noms grecs, on le nomme dodécaèdre rhombique ou rhombo-dodécaèdre, rhombe signifiant losange.
Les autres formes de maille génèrent des formes tronquées plus complexes: pyramides, prismes, rhomboèdres, etc. Les minéralogistes les ont répertoriées au point qu'en regardant la forme macroscopique d'un cristal, ils peuvent deviner la forme de sa maille. De nos jours, la maille est définie sur le plan atomique comme nous allons le voir dans la section suivante. Deux excellents exposés sur les formes des minéraux en relation avec leur maille atomique sont disponibles sur le site de P. Gosse et dans le petit ouvrage détaillé de J. Deferne Introduction à la cristallographie.

Fig.6- Cliché de diffraction de rayons X par un cristal
Les rayons X ont été découverts en 1895 par le physicien allemand Wilhelm Röntgen, premier prix Nobel de physique. C'est en 1912 que Max von Laue (prix Nobel de physique 1914), constatant que les rayons X sont diffractés par les cristaux en faisceaux séparés, pose les bases d'une méthode qui consiste à recueillir le cliché de diffraction d'un faisceau de rayons X par un cristal pour en déterminer la structure atomique.
Sur les clichés de diffraction des cristaux, on voit des séries de taches disposées en rangées symétriques (fig.6). Leur analyse montre que les atomes sont disposés de façon régulière et alignée dans des plans. Chacune des taches correspond à une famille de plans parallèles et équidistants.
La distance entre ces plans est extrêmement petite, inférieure au nanomètre. Un nanomètre est un millionième de millimètre. En nous plongeant dans le monde des atomes, nous effectuons un zoom prodigieux de 10 millions de fois. Inutile de dire qu'avec leurs petits marteaux, les minéralogistes ne pouvaient pas cliver les cristaux à cette échelle.
La régularité avec laquelle les atomes sont empilés est une façon d'occuper un volume réduit. En effet, si nos voulons empiler des oranges de tailles identiques en les tassant au maximum sur une surface plane, elles s'arrangent en lignes décalées (fig.7). De même les atomes se touchent, comme par exemple dans un cristal de sel, qui combine atomes de sodium (Na) et atomes de chlore (Cl) (fig.8).
Toutefois, la réalité des atomes comporte une différence majeure avec celle des oranges: les atomes n'ont pas de surface extérieure bien définie ni un rayon précis. Un atome n'est pas un objet en soi que l'on peut toucher, photographier et mesurer. C'est un modèle, autrement dit une représentation mathématique commode et fructueuse des forces internes de la matière (voir article Matière et rayonnements). C'est pourquoi les images des atomes ne sont que des représentations symboliques.
 | 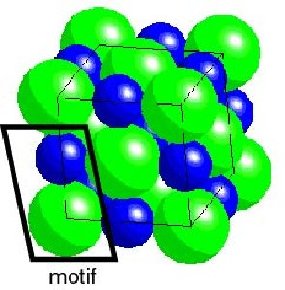 | 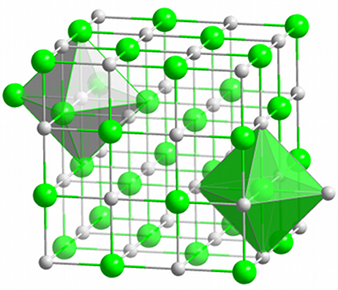 |
| Fig.7- Tassement d'oranges ordonnées en lignes alternativement décalées. © J. Deferne | Fig.8- Empilement cubique d'atomes dans une maille de chlorure de sodium. Dans cette représentation, les ions chlore (en vert) occupent les sommets d'un cube, et les ions sodium (en bleu) occupent le centre des arêtes de ce cube. Un motif répétitif est constitué d'un atome de chlore et d'un atome de sodium (cadre noir). Image Wikipedia | Fig.9- Même réseau cristallin cubique à faces centrées de chlorure de sodium, souligné par des barres. Les ions sodium (en gris) sont répartis en octaèdres autour de chaque ion chlore (en vert) et vice-versa. Image Wikimedia |
La figure 9 montre une autre façon de représenter les atomes. Ils y sont beaucoup plus petits et reliés par des barres. C'est certainement moins conforme à la réalité, car les barres n'ont pas d'existence physique solide. Elles sont seulement un concept abstrait. Dans le domaine de l'infiniment petit, la notion d'objet solide se perd. Les barres sont dessinées pour mettre en évidence les symétries de cet empilement. Toutefois, elles peuvent aussi suggérer les influences électriques entre atomes, leurs liaisons chimiques.
Les résultats du diagramme de diffraction du sel indiquent que les atomes du chlorure de sodium sont disposés en un motif composé d'un atome de chlore et d'un atome de sodium qui se répète de façon périodique (fig. 8 et 9). C'est pourquoi il n'est pas nécessaire de préciser la position de chaque atome du cristal pour le décrire. On peut se contenter de décrire le motif répétitif et dire où on doit le reproduire. C'est l'ensemble des points aux sommets et au centre des faces d'un cube élémentaire (le centre de chaque atome vert sur la figure 8), disposition appelée système cubique à faces centrées.
Il en est de même pour tous les cristaux. Il est possible de décrire totalement un cristal en mentionnant d'une part le motif répétitif et d'autre part le réseau de points sur lequel il est répété.
On peut comparer cette séparation de la position des atomes d'un cristal en deux éléments à la disposition d'un carrelage sur le sol. Le motif répétitif est analogue à un seul carreau. Si on marque sur le sol l'emplacement de chaque carreau, disons en repérant le coin inférieur gauche du carreau par un point rouge, alors on dessine un réseau de points rouges sur lesquels on dépose le motif élémentaire (fig.10).
 | Fig.10- Un carrelage peut être décrit ... | Un même carrelage peut être décrit de plusieurs façons. Plusieurs motifs sont possibles: 3 exemples de mailles simples (comportant un seul motif) sont donnés (cadres rouges). Une maille double est représentée dans le haut. |
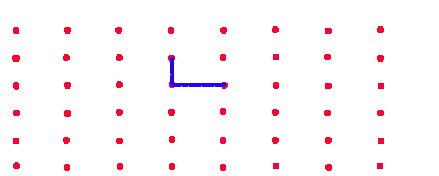 | ... comme un réseau de points dessinés sur le sol, sur lesquels on dépose ... | Les traits bleus sont les arêtes du carreau, les 2 vecteurs de répétition du réseau. |
 | ... un carreau orné de son motif répétitif. |
Tandis que la structure du pavage du sol se déroule sur une surface à deux dimensions, la répétition de la maille cristalline se produit dans l'espace à trois dimensions. La maille est comme une boite dans laquelle est placé le motif, constitué d'atomes et de molécules disposées à des places fixes de la boite. Cette boite peut avoir une forme rectangulaire, droite comme une boite de chaussures. Mais la maille peut avoir d'autres formes avec des angles entre les arêtes différents de l'angle droit. Ce sont des prismes et des formes parallélépipédiques.
De cette description, les scientifiques ont tiré une définition d'un cristal:
Un cristal est un solide à structure polyédrique périodique, formée d'un empilement ordonné d'atomes, de molécules ou d'ions.
La décomposition abstraite des ensembles atomiques cristallins réels en 2 éléments n'est pas unique. Pour un même cristal, il y a différentes façons de définir sa maille. La figure 10 de l'assemblage de carreaux en montre 4 (cadres rouges).
Par exemple, on aurait pu définir un carreau (maille) avec le rond bleu positionné à gauche. Ou bien un carreau qui soit non pas un rectangle, mais un parallélogramme. Examinons cette question sur la figure 11 où chaque point représente un motif sur une surface en deux dimensions. Les mailles vertes sont des exemples possibles de mailles simples comportant un seul motif. On les appelle mailles primitives. On remarque qu'il n'y a pas un choix unique de maille primitive, mais des choix qui nous sont plus ou moins commodes, plus ou moins parlant par leur simplicité. Simplicité signifie peut-être que nous leur trouvons plus de symétrie.
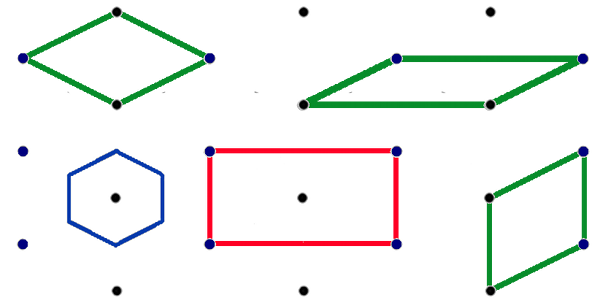 | 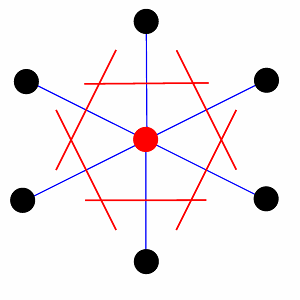 |
| Fig.11- Différents types de mailles dans un réseau rectangulaire centré en 2 dimensions. La maille conventionnelle du réseau (en rouge dans la figure) possède des côtés parallèles aux axes de symétrie du réseau et englobe deux motifs. Les mailles vertes sont des exemples de mailles primitives. En bleu, la maille de Wigner-Seitz. © A. Boudet | Fig.12- Méthode de détermination d'une cellule de Wigner-Seitz. |
La maille rouge nous parle encore plus, car elle montre bien les éléments de symétrie. On la retient comme maille conventionnelle. Mais on remarque qu'elle comporte deux motifs identiques (l'un à un coin représenté en bleu, l'autre au centre représenté en noir). Les motifs des autres coins sont associées aux mailles contigües. C'est une maille multiple.
Il existe toutefois une maille primitive tout-à-fait particulière qui représente parfaitement les symétries internes, c'est la maille de Wigner-Seitz. On la construit autour d'un point du réseau (fig.12, point rouge) en traçant les lignes qui le joignent aux points voisins (lignes bleues). On les coupe en leur milieu par un plan perpendiculaire (lignes rouges). La maille ou cellule de Wigner-Seitz est la figure qui en résulte (en rouge). Si on effectue cette construction dans le cas de la maille rectangulaire centrée de la figure 11, on obtient un hexagone (en bleu).
Ces exemples à deux dimensions nous ont permis de comprendre ce que sont les mailles. Dans le cas des cristaux, il nous faut maintenant les imaginer en 3 dimensions. Nous ferons connaissance avec les différentes géométries des réseaux cristallins, puis nous observerons quelques belles cellules polyédriques de Wigner-Seitz dans l'espace.
Nous laissons maintenant de côté les motifs de la maille primitive pour nous occuper uniquement des points où ils sont disposés, les réseaux. Quels types de réseaux pouvons-nous découvrir dans l'immense variété des cristaux connus. Mon but n'est pas de faire un catalogue, mais de comprendre comment et de nous émerveiller de la façon dont la nature se construit sur des bases géométriques.
Bien avant la description atomique des cristaux, en recherchant mathématiquement les structures qui sont compatibles avec une périodicité dans les trois directions de l'espace, Auguste Bravais (1848) a montré que le nombre de systèmes cristallins possibles était très limité. Il a répertorié 14 types de réseaux qui sont des variantes de seulement 7 systèmes cristallins.
Ainsi dans la nature, seulement 7 formes polyédriques de base, 7 briques élémentaires, permettent de construire l'infinité structurale des minéraux. Toutefois, si leurs formes sont semblables d'un minéral à l'autre, elles varient par leurs dimensions. Longueur, largeur, hauteur d'une maille sont spécifiques à chaque forme chimique cristalline.
Voici ces 14 types de réseaux (fig.13). Leur maille est parfois primitive (P, en bleu) avec un seul site par maille. Si un deuxième site existe au centre de la maille, c'est une maille centrée (I, en vert). Lorsque chacune des 6 faces comportent un site (F, en rouge), ce site étant commun à deux mailles contigües, cela fait 4 sites par maille. On rencontre parfois aussi des mailles avec seulement deux faces centrées (C, en violet), soit 2 sites par maille.
Fig.13- Les 7 systèmes cristallins et les 14 réseaux
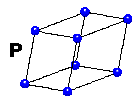 | Le système triclinique est le système le plus général car il englobe tous les autres comme des cas particuliers. Les côtés de la maille (appelés axes) sont obliques. Leurs dimensions (largeur, longueur et hauteur) sont toutes inégales. On peut le décrire comme un prisme incliné dont les 6 faces sont des parallélogrammes. |
|
| Si nous prenons deux de ces axes (ici ceux du plan horizontal) et que nous les écartons pour ajuster l'angle à 90°, nous obtenons le système monoclinique. C'est un parallélépipède incliné avec 4 faces rectangulaires. Les 2 autres sont des parallélogrammes. |
|
| Redressons le 3e axe à la verticale afin qu'il soit à angle droit avec les deux autres et nous obtenons le système orthorhombique. C'est un prisme droit avec 6 faces rectangulaires. |
|
| Continuons nos ajustements en modifiant la longueur des axes. Lorsque deux de ces axes ont une longueur égale, une face devient carrée. Nous obtenons le système quadratique ou tétragonal avec 2 faces carrées et 4 faces rectangulaires. |
|
| Enfin, si le troisième axe a la même longueur que les deux autres, cela devient un cube. C'est le système cubique. |
|
| Le système hexagonal dérive du système orthorhombique en ajustant l'angle de deux axes à 120°. On obtient un prisme droit dont la base est un losange. |
|
| Dans le système rhomboédrique, les trois axes sont de même longueur et les trois angles sont égaux, mais non droits. Les faces sont toutes des losanges (des rhombes). |
Il existe un lien entre la géométrie de ces réseaux à l'échelle atomique et la géométrie des cristaux visibles à l'œil nu. En effet, lorsqu'on le clive, le cristal se fractionne le long des plans atomiques qui contiennent les atomes en plus grande quantité, autrement dit les plans simples de la maille (fig.14). Les facettes extérieures sont donc la manifestation macroscopique des plans atomiques microscopiques.
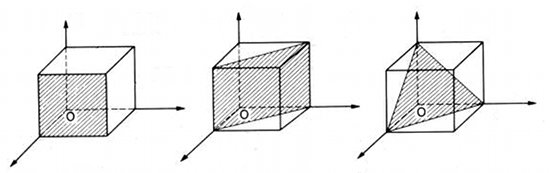
Fig.14- Plans de clivage (hachurés) du système cubique
La maille de Wigner-Seitz (WS) est découpée dans l'espace à trois dimensions selon le procédé exposé plus haut en deux dimensions. Elle est très intéressante du point de vue géométrique.
En effet, puisque pour le dessiner on trace un plan entre deux sites du réseau, cela délimite le territoire de chacun des sites. La cellule étant limitée par des plans, c'est par définition un polyèdre. On a ainsi découpé l'espace en polyèdres identiques. Ces polyèdres se touchent et leur empilement remplit donc complètement l'espace, sans aucun vide (voir en annexe Remplir l'espace).
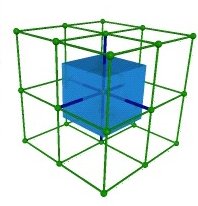
Fig.15- Maille de Wigner-Seitz du réseau cubique simple: un cube
Merci à Laura Malcolm
Puisqu'on construit le polyèdre autour d'un site et qu'on tient compte de tous les sites voisins, il reflète parfaitement les symétries du réseau.
Illustrons cette géométrie dans le cas du système cubique.
La maille WS du réseau cubique simple est un cube qui reflète le cube de la maille conventionnelle (fig.15). Les cubes s'empilent parfaitement les uns avec les autres.
Pour dessiner la maille WS du réseau cubique centré (fig.16), partons du site central (en rouge), et imaginons la ligne (en rouge) qui le relie au site central du cube voisin. Le plan qui les sépare à mi-distance est la face du cube (en vert). Les 6 faces du cube conventionnel appartiennent donc à ce polyèdre. Elles sont tronquées par les plans qui séparent le site central des sommets, soit 8 autres faces (en bleu).
Au total, on a un cube à 6 faces carrées tronqué par 8 faces hexagonales, soit 14 faces au total (fig. 16). Il peut être considéré comme un octaèdre (les 8 faces bleues - voir fig.4) dont les sommets sont tronqués par les 6 autres (vertes) (fig.17).
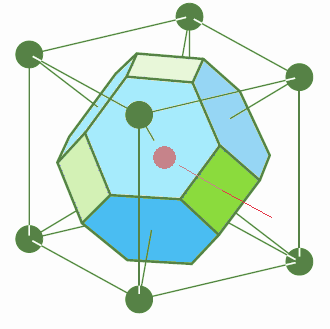 | 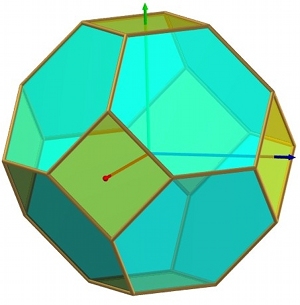 | 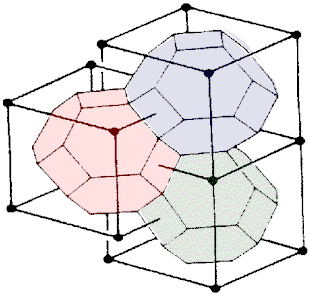 |
| Fig.16- Maille de Wigner-Seitz du réseau cubique centré: un octaèdre tronqué. © A. Boudet | Fig.17- Belle représentation d'un octaèdre tronqué. Merci à Mathcurve | Fig.18- Empilement d'octaèdres tronqués dans le réseau cubique centré. Merci à Laura Malcolm |
Comme prévu, lorsqu'on les empilent, ils s'ajustent parfaitement pour remplir l'espace sans vide (fig. 18).
Dans le réseau cubique à faces centrées, le centre n'est pas occupé par un site. Pour dessiner la maille, on part d'un site au centre d'une face du cube conventionnel (en rouge, fig.19). Ses plus proches voisins sont situés sur les centres des faces de ce cube et à ses sommets. Ils dessinent un autre cube décalé par rapport au premier (en vert) et sont situés au milieu des 12 arêtes de ce nouveau cube. Ils sont au nombre de 12.
Si nous traçons les plans perpendiculaires aux lignes qui joignent le point central à ces 12 proches voisins, nous obtenons 12 faces losanges. C'est un dodécaèdre (12 faces) rhombique (losanges).
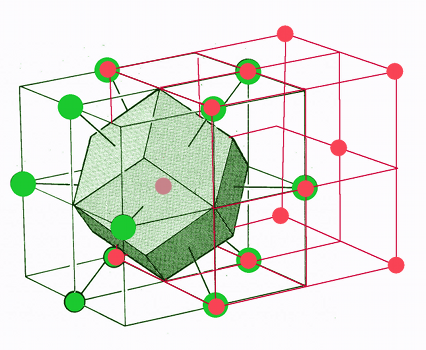 | 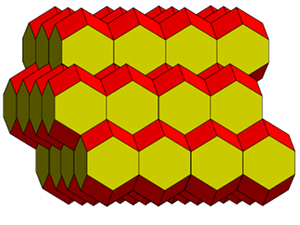 |
| Fig.19- Maille WS du réseau cubique à faces centrées: le dodécaèdre rhombique © A. Boudet Voir aussi Mathcurve | Fig.20- Maille WS du système tétragonal centré: le dodécaèdre rhombo-hexagonal. Empilement de dodécaèdres rhombo-hexagonaux en "nid d'abeille" |
Nous avons déjà rencontré le dodécaèdre rhombique plus haut (fig.5) comme cube dont on a tronqué les arêtes. Il n'est pas régulier car ses sommets ne sont pas tous identiques. 8 sommets sont d'ordre 3 (3 arêtes en partent) et 6 sommets sont d'ordre 4. Leur empilement est bien entendu parfaitement ajusté dans l'espace à 3 dimensions.
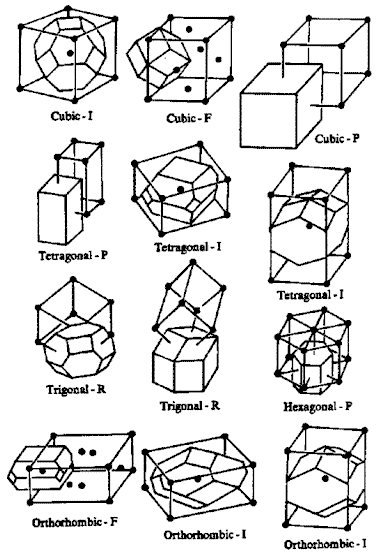
Fig.21- Merci à Laura Malcolm
Les autres réseaux résultent du cube en l'étirant dans un sens ou dans l'autre. Par exemple, si on tire sur deux faces opposées, le cube devient un parallélépipède rectangle, donc on a le système tétragonal.
En conséquence, la maille WS du système tétragonal résulte d'un étirement de la maille WS du système cubique. Ainsi, la cellule WS du système tétragonal centré est un dodécaèdre rhombique étiré. Certaines des faces losangiques s'étirent en hexagone. On obtient le dodécaèdre allongé ou dodécaèdre rhombo- hexagonal.
Le dodécaèdre rhombo-hexagonal comporte toujours 12 faces, dont 8 sont des losanges et 4 des hexagones équilatéraux.
Nous vérifions (fig.20) que leur empilement est parfaitement ajusté dans l'espace à 3 dimensions.
La figure 21 montre les polyèdres obtenus pour les autres systèmes à partir du cube par déformation globale, soit en l'étirant, soit en l'inclinant.
Les formes polyédriques des mailles cristallines existantes sont en nombre limité. On peut montrer géométriquement que les polyèdres capables de s'empiler par translation périodique pour remplir tout l'espace doivent obéir à certaines règles simples de symétrie (voir en annexe Remplir l'espace). Certaines formes de polyèdres ne conviennent pas pour un tel empilement parce qu'elles laissent des vides entre elles, comme les oranges de la fig.7. C'est par exemple le cas des prismes à 5 faces (pentagonaux) et des polyèdres à symétrie d'ordre 5.
On dit qu'une forme possède une symétrie d'ordre 5 autour d'un axe si, lorsque vous la tournez d'1/5 de tour, vous retombez sur la même forme. Par exemple, un cube possède la symétrie d'ordre 4 par rapport à un axe qui traverse le centre de 2 faces opposées.
Or au début des années 1980, malgré cette impossibilité théorique, on a obtenu par trempe rapide des alliages d'aluminium et de manganèse dont le diagramme de diffraction aux rayons X est bien net et montre bel et bien la symétrie 5. Au début, cela a beaucoup intrigué (fig.22). Cette découverte et son analyse ont élargi le concept géométrique du cristal.
Pour expliquer l'existence de cette symétrie, il faut associer deux polyèdres différents et non un seul dans la construction. Pour se représenter cette association de façon plus claire, examinons comment c'est possible à deux dimensions, donc sur une surface plane. Cela a été étudié par des mathématiciens sous le terme de pavage de l'espace.
Voici un exemple de pavage étudié par Roger Penrose utilisant deux types de losanges (fig.23, les verts et les jaunes). Il est à remarquer qu'ils ne sont pas pas orientés dans la même position. Il n'y a donc pas de régularité de translation. De plus, aucune périodicité n'est visible, même avec des motifs géants. Et pourtant, c'est un assemblage compact construit selon un ordre rigoureux. La symétrie qui en résulte est d'ordre 5.
 | 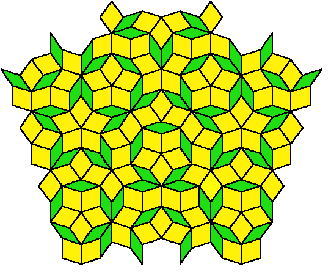 |
| Fig.22- Diagramme de diffraction d'un quasi-cristal de symétrie 5. Merci aux chimistes de l'Université Louis Pasteur de Strasbourg | Fig.23- Un pavage du plan avec deux types de losanges inventé par R. Penrose. Pour plus de détails, voir Pavage de Penrose |
Ces constructions géométriques en 3 dimensions qui ont une régularité précise, mais ne présentent pas de périodicité de translation sont appelées des quasi-cristaux. Comme le montre le diagramme de diffraction faits de points disposés selon de belles symétries (fig.22), un ordre y est à l'œuvre. Mais quel est cet ordre?
Il existe plusieurs façons de répondre à cette question. Si nous prenons comme exemple le pavage de Penrose, la première façon est de donner le mode de réalisation du dessin (voir Pavage de Penrose). La deuxième est de décrire le pavage, non dans son espace réel de dimension 2 (la surface) mais dans un espace plus vaste de dimension 4. Dans celui-ci, le pavage peut être décrit comme périodique, donc de façon bien plus simple (voir en annexe Décrire une réalité dans un super-espace). De la même manière, un quasi-cristal devient périodique quand il est décrit dans un super-espace de dimension 6.
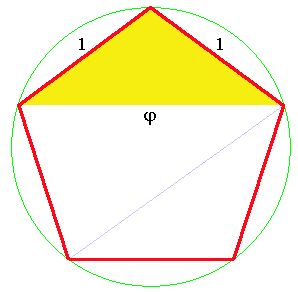
Au passage, je signale pour les amateurs que dans ce pavage, on rencontre le nombre d'or. C'est tout-à-fait logique car ce nombre est associé à la symétrie 5. Il vaut (1+√5)/2. On le désigne habituellement par la lettre φ (phi). Si on dessine un pentagone régulier (tous les côtés et les angles ont la même valeur) dont le côté mesure 1, on trouve le nombre φ sur la diagonale (fig.24). Les triangles qui sont construits sur cette diagonale sont appelés triangles d'or. Il en existe 2 sortes, l'une dont l'angle est aigu (en bleu) et l'autre dont l'angle est obtus (en jaune). Et bien (ce n'est pas un hasard), les losanges du pavage de Penrose sont constitués de l'assemblage de ces 2 triangles (voir les détails dans Pavage de Penrose).
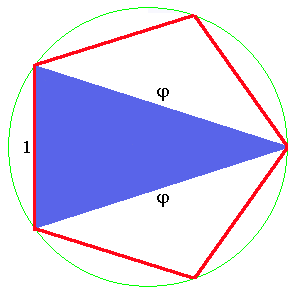 |  |
| Fig.24- Les triangles d'or sont inscrits dans un pentagone régulier. La diagonale a pour longueur φ=(1+√5)/2 | |
Après la découverte historique d'un quasi-cristal à symétrie 5, d'autres structures quasi-cristallines ont été reconnues. En conséquence, en 1992 l'Union internationale de cristallographie a modifié sa définition d'un cristal pour englober celle d'un quasi-cristal. Dorénavant, un cristal est un échafaudage atomique dont la diffraction est faite de points qui traduisent un ordre précis de construction. Mais cet ordre peut être une périodicité ou non.
A la même époque, on commençait à étudier d'autres types de cristaux apériodiques, les cristaux incommensurables. Pour comprendre de quoi il s'agit, imaginons une périodicité sur une seule ligne, une sorte de cristal à une seule dimension (fig.25). Un cristal classique périodique est représenté par les points bleus, placés selon une périodicité a. Imaginons maintenant que les points du réseau sont décalés par rapport aux points bleus (d'une distance un). Leur position réelle est le point rouge. On remarque que le décalage varie de façon périodique, selon une périodicité λ. Il existe donc 2 périodicités, la bleue (a) et la rouge (λ). Si ces deux sont en rapport, elles vont coïncider régulièrement et on aura une périodicité globale qui sera un multiple des deux. On dit qu'elles sont commensurables. Si les deux n'ont pas de rapport entre elles, ne sont pas multiples l'une de l'autre, ou n'ont pas un multiple commun, elles sont incommensurables. Le décalage ne tombera jamais à la même valeur.
 Fig.25- Représentation d'un cristal incommensurable sur une ligne. Les sites existants (en rouge) peuvent être décrits comme un site théorique (en bleu) qu'on déplace d'une quantité un. La position des sites bleus est un multiple de a, et la longueur de un varie selon une périodicité λ. D'après S. Ravy
Fig.25- Représentation d'un cristal incommensurable sur une ligne. Les sites existants (en rouge) peuvent être décrits comme un site théorique (en bleu) qu'on déplace d'une quantité un. La position des sites bleus est un multiple de a, et la longueur de un varie selon une périodicité λ. D'après S. Ravy
Un cristal incommensurable est donc apériodique, mais dans cette apériodicité se cachent deux périodicités qui se combinent. Pour le décrire mathématiquement, comme les quasi-cristaux, il est beaucoup plus simple de le faire dans un espace de dimension supérieure (4 à 6 dimensions) (voir en annexe Décrire une réalité dans un super-espace).
En 1972, De Wolf et Van Aalst ont mis en évidence des domaines incommensurables à 3 dimensions dans des cristaux de carbonate de soude. D'autres ont été reconnus par la suite.
Changeons de paysage. Après avoir observé les étonnants arrangements géométriques des cristaux à l'échelle atomique, nous pouvons nous poser certaines questions: comment la matière minérale peut-elle ainsi s'organiser de façon aussi ordonnée? Par quel processus, entrainés par quelle forces, les atomes sont-ils ainsi disposés?
Dans le liquide, les atomes (ou les molécules constitutives qui sont des petits groupements d'atomes) sont libres de se déplacer les uns par rapport aux autres, tandis qu'en devenant un corps solide comme un cristal, ils sont immobilisés dans un réseau.
Notre expérience la plus familière d'une cristallisation est celle de l'eau dans laquelle apparaissent des glaçons lorsqu'on la refroidit en-dessous de 0 degrés C. On passe d'un état fluide léger à un état rigide et dur.
Dans le langage courant, on parle de cristallisation de façon plus générale pour évoquer quelque chose qui au départ est fluide, puis se fixe et durcit. Des idées se cristallisent dans l'esprit, ce qui signifie que l'esprit devient rigide sur certains points. En ce qui concerne le corps, des cuirasses (ou armures) musculaires se forment lorsque des énergies cessent de circuler dans les tissus et s'y cristallisent, provoquant des contractures et la rigidification des tissus (voir Psychologie biodynamique). On parle également de cristallisation pour décrire quelque chose qui, d'abord flottant et indéterminé, se matérialise et prend une forme tangible.
La transformation existe dans l'autre sens, du cristal au liquide. Lorsqu'on les chauffe, les cristaux fondent et deviennent liquides. La plupart des matières minérales, y compris les roches et les métaux, peuvent fondre lorsqu'on les chauffe. En ce qui concerne les métaux, on les fond en un liquide visqueux pour les verser dans des moules où ils prennent les formes voulues. Mais cette température de fusion peut parfois être très élevée: environ 1500 °C pour le fer, 1000 °C pour le cuivre et l'or, 960 °C pour l'argent. L'aluminium fond à une température plus basse (660 °C). Ce sont le plomb (327 °C) et l'étain (230 °C) qui sont les plus faciles à fondre. En refroidissant, les métaux cristallisent dans des structures et configurations qui dépendent à la fois de leur nature chimique, mais aussi beaucoup du processus de refroidissement, en particulier de la vitesse de refroidissement.
Les roches fondent lorsqu'on les chauffe suffisamment. La nature nous le démontre avec la lave qui sort liquide de dessous la croute terrestre, se refroidit en surface et cristallise. Mais ce refroidissement rapide ne favorise pas la formation de beaux cristaux. Les pierres d'ornement se forment par d'autres processus dans la profondeur de la terre, où la pression est associée à la chaleur et le refroidissement lent. En surface, dans les grottes, elles résultent du lent dépôt par l'eau de substances minérales sur un petit bout de cristal existant (un germe).
Comment passe-t-on d'un état liquide où les molécules sont mobiles et dispersées en désordre, à un cristal ordonné? Dans les liquides tels que l'eau, l'huile ou un métal en fusion, les molécules se déplacent librement les unes par rapport aux autres. Si on les représente par des boules, on peut les imaginer glissant et roulant les unes sur les autres. Et puis, au signal d'une température suffisamment basse, les voilà qui se rangent en ordre impeccable selon des lignes, des plans et des mailles. Quel en est le ressort?

Pour en donner une idée, imaginons que les molécules sont comme des personnes, nous. Nous assistons à un cours de gymnastique ou de danse où les personnes sont dispersées dans toute la salle, en désordre, pour remplir l'espace au maximum. Du point de vue d'une molécule, nous sommes "dans l'état liquide", car nous avons la liberté de nous mouvoir, de nous retourner (si notre attention n'est pas dirigée vers le professeur), de changer de place, d'échanger notre place avec une autre personne, etc.
Puis, le professeur nous demande de nous disposer en ligne. Comment nous y prenons-nous? Quelques personnes au fond de la salle commencent à se mettre en ligne parallèlement au mur. Il est nécessaire que quelqu'un prenne l'initiative, donne la première impulsion afin que les autres, progressivement, s'ordonnent par rapport à cet embryon de ligne. La ligne se prolonge sur toute la longueur de la salle. En même temps, une autre ligne se crée devant la première et parallèlement à elle. Et une troisième, même si la première et la deuxième ne sont pas achevées.
Il en est de même pour un cristal. Dans le liquide, un cristal se forme à partir d'un germe qui nait et grossit (cristallogenèse). On distingue donc deux étapes. La germination correspond à l'apparition d'un germe cristallin dans le liquide, sorte de semence ou d'embryon cristallin. Si aucun germe n'est présent, la cristallisation a du mal à démarrer et le liquide peut être refroidi sans cristalliser. C'est un liquide surfondu. Et puis, peut-être à cause d'une petite secousse, le refroidissement devient intolérable pour les molécules et brusquement, un germe se forme.
Refroidir, c'est serrer les molécules encore plus les unes contre les autres. Imaginez que la salle se remplisse de monde et que vous deveniez serrés. Vous devrez vous rapprocher et si vous êtes en contact, il y aura une sorte d'ordre local qui va se créer automatiquement pour quelques personnes, à la façon des oranges de la fig.7. En même temps, il sera plus difficile de se déplacer.
La croissance est l'augmentation de la taille du germe pour devenir un cristal. Oui, un cristal nait et se développe un peu comme un être vivant. Il grossit en incorporant d'autres molécules qui passent à sa proximité dans le liquide ambiant et se collent à la surface au contact les unes des autres (fig.26).
Pour obtenir un cristal d'une substance donnée, on peut, comme on l'a dit, la fondre puis la refroidir. Il y a aussi la possibilité de la dissoudre dans un solvant, puis de laisser évaporer ce solvant. C'est ce qui se produit avec du sel. Si vous dissolvez du sel dans de l'eau en quantité suffisante (eau saturée de sel) et que vous laissez l'eau s'évaporer lentement, vous obtenez des cristaux de sel.
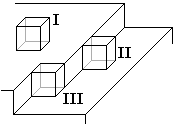 | 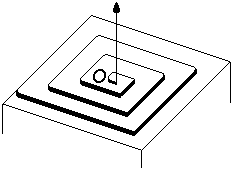 |
| Fig.26- Schéma de déposition de nouvelles molécules ou atomes (représentés par des cubes) à la surface d'un germe cristallin en terrasse. D'après Raphaël, Aude et Benoît | Fig.27- Croissance en spirale à la faveur d'une dislocation qui émerge en surface au point O. |
On a donné des cristaux l'image d'un ordre parfait, mais ce n'est pas exact. En réalité, cet ordre comporte des exceptions, qu'on appelle des défauts.
Il se peut que des atomes étrangers s'insèrent dans l'arrangement. Quelquefois un atome est manquant. C'est comme si, d'une rangée à l'autre, l'ajustement ne se fait pas correctement. Imaginons que notre ligne de danse ne se soit pas correctement positionnée par rapport à la précédente, qu'elle ne soit pas vraiment calée. C'est ce qui arrive souvent dans un cristal. Ce défaut est appelé une dislocation.
Ce ne sont des défauts qu'au sens d'un ordre parfait, d'une vision idéale. Car ces soi-disant défauts ont toute leur raison d'être dans l'organisation, les caractéristiques et la croissance des cristaux. Ils y participent pleinement. C'est grâce à la présence de dislocations que les métaux peuvent être déformés et travaillés. C'est aussi la présence des dislocations qui donne à la croissance cristalline la possibilité de se faire plus aisément, du point de vue énergétique, sous forme de spirales (fig.27 - voir article Spirale, mouvement primordial de vie).
Revenons à notre salle de danse. Imaginez maintenant que le professeur n'ait pas une place attitrée dans la salle, donc qu'on n'impose pas à la ligne de s'orienter dans une direction précise pour le regarder. Imaginez alors que le début d'une première ligne se forme dans une certaine direction, mais qu'ailleurs dans la salle, un autre embryon de ligne n'ayant pas vu le premier, se forme dans une orientation différente. Les personnes qui sont proches de la première ligne viennent la compléter, s'ordonnent par rapport à elle, constituent d'autres lignes parallèles. Un domaine ordonné se forme dans un coin. De même pour la deuxième ligne. Les domaines respectifs issus de ces deux lignes s'agrandissent jusqu'à se rencontrer. Le raccord entre les deux ne peut pas se faire en ordre et il y a une frontière désordonnée entre les deux domaines. Imaginons qu'une troisième ligne se soit formée de façon indépendante. Trois domaines d'orientations différentes se sont ainsi formés, comme si on avait trois cristaux distincts qui sont accolés.

Fig.28- Surface de granite. Son nom vient de sa structure en grains, bien visibles à l'œil nu: quartz, mica et feldspaths. Merci à Wikimedia
C'est ce qui se produit dans la structure cristalline de beaucoup de roches et de matériaux céramiques, métalliques et polymères. Ces matériaux sont polycristallins. Dans certains matériaux, les domaines cristallins sont de la même nature, mais dans d'autres ils peuvent être de nature différente. Ainsi, le granite est fait d'une multitude de petits grains cristallins de quartz, de feldspath et de mica (fig.28).
Ces matériaux faits de grains agglomérés ont des formes indéterminées. La forme extérieure ne laisse pas deviner l'arrangement cristallin intérieur.
Autre exemple, le quartz. Alors que sous la forme populaire de prisme transparent, il est monocristallin, il existe également sous la forme multicristalline de la calcédoine (voir en annexe Quartz). Elle est translucide ou opaque car faite d'une multitude de petits cristaux orientés dans tous les sens.
La structure polycristalline résulte de la présence d'une multitude de germes dans le liquide ou le magma initial. Au refroidissement, chaque germe grandit en un domaine cristallin jusqu'à toucher le domaine voisin. La taille d'un domaine est limitée par le territoire occupé par les germes voisins. C'est pourquoi plus les germes sont nombreux, plus les domaines cristallins sont petits.
Dans certains cas, les cristaux d'un minéral polycristallin sont microscopiques et invisibles à l'oeil nu ou même à la loupe. C'est le cas des métaux dans certaines conditions de cristallisation, et des polymères cristallins, dont les formes externes, qui épousent n'importe quel moule, ne laissent pas deviner leur nature cristalline. Seules les diffractions des rayons X ou des électrons, qui donnent accès à l'information au niveau atomique, sont capables de révéler leur nature cristalline.

Obsidienne. Merci à Wikipedia
Lorsqu'on refroidit le liquide, les molécules constitutives de ce liquide perdent leur liberté de mouvement. Quelquefois, en l'absence de germes cristallins, le liquide "oublie" de cristalliser et se fige dans son état du moment. C'est un peu comme si nos lignes de danseurs ne sont plus dans une salle mais dans un bain visqueux qui entrave leurs mouvements. Alors, ils ne peuvent que rester sur place, en désordre.
Cette structure désordonnée est appelée structure amorphe. Les liquides visqueux ont également cette structure amorphe. Avec le froid, une huile se fige sans cristalliser. Toutefois, dans l'état visqueux, la structure amorphe reste un peu mouvante. Lorsque les mouvements moléculaires s'arrêtent, on la nomme structure vitreuse.
Vitreuse signifie de la nature du verre. En effet, les verres présentent cette structure vitreuse. Ce sont des pâtes de silice refroidies rapidement (voir en annexe Silice). On les obtient en fondant ensemble du sable et des fondants (chaux, potasse ou soude). Le refroidissement rapide ou trempe favorise la formation de cette structure, car les molécules sont immobilisées avant d'avoir eu le temps de s'organiser.
Pour donner une image plus correcte de l'état vitreux, notons toutefois que la matière n'est jamais figée complètement. Si les molécules ne bougent plus, par contre les atomes dont elles sont composés conservent un intense mouvement vibratoire sur place. Ils rayonnent. La matière est en constante vibration et détient une formidable énergie interne.
Parmi les pierres gemmes, certaines sont à l'état vitreux. C'est le cas de l'obsidienne, une roche volcanique à base de silice. C'est le cas de l'ambre, une résine fossilisée secrétée par des conifères.
Le passage de l'état de liquide à celui de cristal est un changement radical. Le liquide est fluide et s'adapte au récipient dans lequel on le met, il n'a pas de forme en lui-même. Le cristal est compact et dur et conserve la forme dans laquelle il a été taillé. On passe d'une qualité à son opposé et c'est étonnant.
Pourtant, le changement le plus spectaculaire dans ce passage est celui de l'ordre atomique et moléculaire. De ce point de vue, il y a peu de changement entre un liquide et un verre (état amorphe) qui n'est qu'un liquide figé, alors qu'il y a un changement radical entre un liquide et un cristal. Si l'on y réfléchit, c'est une métamorphose fantastique. Il suffit d'un déclencheur, d'une pichenette, un petit refroidissement, et la mise en ordre s'effectue.
Dans cette métamorphose, certaines substances passent par des étapes intermédiaires entre liquide et cristal. Ce sont les cristaux liquides. Dans les états intermédiaires, on détecte un ordre partiel, de telle sorte qu'ils sont liquides par certains aspects, mais ordonnés selon d'autres (voir Cristaux liquides).
Qu'est-ce qui induit la géométrie de l'ordre cristallin au moment du changement? Comment le cristal choisit-il son orientation dans un espace qu'on peut supposer isotrope, c'est-à-dire sans aucune direction privilégiée? L'espace ressemble à une vaste mer, et soudainement, une orientation cristalline se fait jour. Pourquoi celle-ci?
C'est un mystère profond de la nature dont on connait peu de choses. Le phénomène obéit aux forces fondamentales et aux symétries internes de la nature. Il se peut que l'univers soit sous-tendu par des structures géométriques, y compris notre corps et le corps de la Terre. Je décris scientifiquement cette possibilité dans d'autres articles (La grille planétaire; Aspects géométriques et sonores de l'Univers).
Le diamant est très apprécié en joaillerie comme pierre précieuse, mais tout autant dans l'industrie et l'artisanat mécanique pour sa dureté. Il y est employé pour découper et percer des matériaux durs. Le mot diamant vient du latin adamas, qui signifie inaltérable.
Les diamants, tout comme comme le quartz, présentent un double caractère cristallin par leur transparence et par leur géométrie atomique ordonnée. Ce sont donc des cristaux typiques.
Le diamant est composé uniquement d'atomes de carbone. C'est assez exceptionnel car généralement, les minéraux sont faits d'un assemblage de plusieurs types d'atomes. Ainsi, le quartz est composé d'atomes de silicium et d'oxygène. Seuls le diamant et les métaux sont composés d'un seul type d'atomes. Par exemple, l'or est composé uniquement d'atomes d'or.
 | 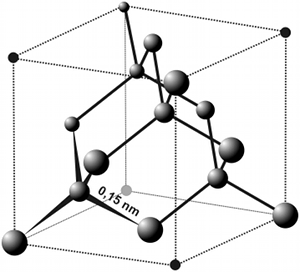 |
| Diamant | Fig. 29- Structure atomique cubique du diamant. Les atomes représentés sont des atomes de carbone. |
Chaque atome de carbone est lié à 4 atomes de carbone voisins par des liaisons qui forment un tétraèdre régulier (fig.29). Ces liaisons très solides confèrent au diamant une structure tridimensionnelle extrêmement rigide. Le diamant cristallise dans le système cubique.
Le graphite est une substance grise et tendre que l'on peut facilement réduire en poudre. C'est grâce à cette facilité qu'il est utilisé dans les crayons ordinaires à papier avec une mine en graphite. Il sert aussi de lubrifiant sec, à la manière du talc. Il est conducteur de l'électricité à tel point qu'on s'en sert comme électrode. On l'emploie aussi comme charge minérale dans les matières plastiques et les caoutchoucs. Pour fabriquer un composite à particules de carbone, on disperse les microparticules de graphite dans la résine afin d'augmenter ses qualités mécaniques et électriques. Elles lui donnent sa teinte grise ou noire. Ils sont employés dans la fabrication des skis, cannes à pêche, raquettes de tennis, ailes d'avion, pièces de carrosserie.
Or le graphite est composé uniquement de carbone tout comme le diamant. Bien que graphite et diamant soient composés des mêmes atomes, leurs propriétés sont opposées (mou / dur, conducteur / isolant, opaque / transparent). Comment est-ce possible? Ce qui diffère est la façon dont ces atomes sont reliés, leur système cristallin. Le graphite se forme en couches planes dans lesquelles les atomes sont liés fortement et ordonnés en réseau hexagonal (fig.30). Par contre, les couches sont très faiblement liées les unes aux autres, ce qui explique qu'elles peuvent facilement glisser les unes sur les autres et se défaire.
Ce sont les conditions de cristallisation qui conduisent à une ou l'autre forme. Le diamant se forme sous une grande pression, et le graphite à faible pression.
 | 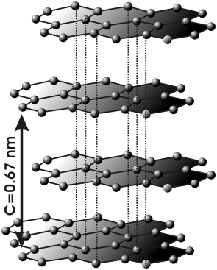 |
| Morceau de graphite | Fig. 30- Structure atomique en couches du graphite |
Le quartz est bien connu en tant que pierre d'ornement dans sa forme de prismes transparents et bien développés. Or il est également un abondant constituant des roches de la croute terrestre. Il est constitué de silice de formule chimique Si02, soit un atome de silicium (Si) pour 2 atomes d'oxygène (O).

Gerbe de quartz, La Gardette, France (Muséum de Genève)
Merci à J. Deferne

Jaspe. Merci à Wikipedia
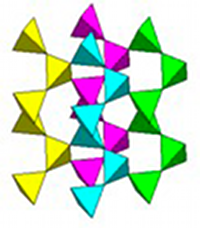
Fig. 31- La silice est faite d'un assemblage de tétraèdres. Chaque tétraèdre est constitué d'un atome de silicium entouré de 4 atomes d'oxygène. Dans le quartz, ils s'assemblent en spires hélicoïdales. Merci à J. Deferne
Le cristal de quartz mérite ce qualificatif de cristal à la fois par son ordre atomique et par sa transparence. Comme le diamant, il est le type même du cristal, au point qu'on le nomme cristal de roche, ou parfois même tout simplement cristal. Ces cristaux magnifiques se développent dans les fissures des roches dans la chaleur de l'intérieur de la terre. Des eaux très chaudes y déposent de la silice qui refroidit lentement, ce qui favorise sa croissance régulière.
Certaines gemmes sont des variétés de quartz coloré par des atomes étrangers insérés en faible quantité parmi les atomes de silicium et d'oxygène. Par exemple l'améthyste est du quartz teinté d'oxyde de fer (Fe2O3). Sa couleur varie du mauve au violet. Il existe aussi du quartz rose, de la citrine jaune, et d'autres...
Le jaspe contient de 80 à 95 % de silice et de l'argile. Le jaspe rouge est coloré par des argiles ferrugineuses. L'œil-de-tigre marron rayé est formé de crocidolite (famille de l'amiante) enrobée dans du quartz.
Il faut que la température de la solution de silice soit assez élevée pour que le quartz cristallise en de beaux cristaux transparents. Lorsque la température est plus basse, il se forme un quartz polycristallin blanc laiteux constitué de nombreux petits cristaux orientés dans tous les sens. A plus basse température encore, la silice forme des encroûtements de calcédoine ou d'opale.
La calcédoine est microcristalline, translucide avec une coloration uniforme grise, bleuâtre ou verdâtre, ou encore rouge (cornaline) ou verte (chrysoprase). Le silex est une roche siliceuse très dure constituée de calcédoine presque pure et d'impuretés telles que de l'eau ou des oxydes, ces derniers influant sur sa couleur. L'agate est constituée de fines couches concentriques de calcédoine diversement colorées. L'opale n'est pas cristalline, mais constituée de minuscules sphères de silice amorphe.
Le quartz forme près de 13 % de la croûte terrestre sous la forme de petits cristaux translucides et grisâtres dans les roches granitiques. Sous l'effet de l'érosion, le granite se désagrège, les grains de quartz sont libérés et contribuent à former le sable des rivières, des lacs et des océans. Selon les conditions environnementales, ces grains peuvent s'agglomérer pour participer à la formation de grès, de quartzite, de gneiss et de schiste.
Le quartz est l'une des variétés de silice qui existe aussi sous d'autres formes dans la nature. On désigne sous le nom de silice la combinaison chimique du silicium et de l'oxygène, SiO2. Elle est soit cristalline (quartz, tridymite, cristobalite), soit amorphe. Le quartz est la forme la plus abondante de façon naturelle.
La silice est le principal constituant des silicates, une combinaison de silice et d'atomes d'autres éléments (aluminium, fer, magnésium, calcium, sodium, potassium). Les silicates sont les constituants majoritaires de l'écorce terrestre.
Le sable résulte de la désagrégation naturelle des roches sous l'effet des agents atmosphériques. Les termes sable et gravier se réfèrent à la taille des grains plus qu'à sa composition chimique. Il existe des sables de quartz et de feldspath.
La silice cristallise sous plusieurs formes minérales en fonction de la température et de la pression. Outre le quartz, on la trouve sous forme de cristobalite, présente dans les roches volcaniques. Elle coexiste avec la tridymite, une autre forme de silice cristalline, rare à l'état naturel, qu'on rencontre dans les matériaux réfractaires industriels, où elle s'est formée sous l'effet de la chaleur.
La silice est largement utilisée dans le domaine industriel. Comme matière première pour la verrerie, la cristallerie, la céramique; à cause de sa transparence, pour l'optique; comme isolant électrique, elle est employée en électronique. Elle est utilisé comme charge minérale dans les plastiques et caoutchoucs où elle améliore leurs propriétés physiques. Enfin, à cause de sa dureté, le quartz est employé comme moyen de sablage, d'abrasion, de sciage, de ponçage, etc.
Dans la silice, les atomes se regroupent en tétraèdres SiO4 dans lesquels l'atome de silicium est situé au centre, relié à 4 atomes d'oxygène placés aux sommets du tétraèdre. Ces tétraèdres sont chimiquement solides et forment les unités stables de la construction atomique. Ils s'assemblent par leurs sommets de sorte que chaque atome d'oxygène est l'articulation entre deux tétraèdres. C'est le type d'assemblage des tétraèdres qui varie et donne diverses formes cristallines de la silice.
Dans la silice vitreuse, les tétraèdres sont empilés de façon désordonnée, tandis que dans le quartz et la cristobalite l'empilement est régulier.
Dans le quartz, les tétraèdres s'articulent en spires hélicoïdales parallèles à l'axe de symétrie vertical du cristal (fig. 31). Selon les variétés de quartz, ces spires s'enroulent soit vers la droite, soit vers la gauche, et on a donc du quartz droit et du quartz gauche, qui se trouvent en quantités équivalentes dans la nature.
Selon les conditions de cristallisation du quartz synthétique, on obtient la forme α trigonale à basse température et la forme β hexagonale à haute température. Entre les deux, il existe une phase incommensurable à 573 °C, stable sur un intervalle d'environ 1,5 °C.
Les cristaux de quartz et quelques autres matériaux ont une propriété électrique étonnante. Lorsqu'on exerce une pression mécanique, ou une autre déformation telle que flexion ou torsion, sur un cristal de quartz, une charge électrique (une tension électrique) apparait sur ses faces. Ce phénomène est nommé effet piézo-électrique (grec piezein, presser). Il est utilisé dans des applications courantes comme l'allume-gaz piézo-électrique et le microphone. Dans le microphone, le son, qui se manifeste comme des variations de la pression de l'air (voir article Nature du son), excite un cristal de quartz qui le transforme en un courant électrique qui est ensuite amplifié.
L'effet inverse a également lieu. Lorsqu'on applique une tension électrique sur les faces d'un cristal de quartz, il se déforme faiblement (quelques millièmes de mm). De cette façon on peut produire des ultrasons.
L'application la plus courante du quartz, l'oscillateur électronique, combine les deux effets pour créer une oscillation mécanique du cristal à une fréquence précise qui dépend essentiellement de sa forme et de ses dimensions. Les quartz sont des composants électroniques très répandus conçus pour vibrer à des fréquences allant de la dizaine de kilohertz à quelques dizaines de mégahertz. Le plus souvent en quartz synthétique, ils sont destinés aux montres à quartz, et aux circuits électroniques en tant que générateurs de fréquences.
Le silicium n'existe pas naturellement à l'état pur. Il est un constituant de la silice, très abondante dans la nature. On peut donc en extraire le silicium chimiquement et le produire sous forme de cristaux (fig.32).
Les cristaux de silicium sont largement répandus dans notre environnement technologique. Dans les panneaux solaires, ce sont des cristaux de silicium qui transforment la lumière en courant électrique (effet photo-électrique) et les puces de nos appareils électroniques sont fabriquées sur un support de silicium cristallin.
 | |
| Fig.32- Barreau de silicium polycristallin, destiné à la production de silicium monocristallin (longueur 10,3 cm, diamètre 4 cm). Merci à Wikipedia | Fig.33- Microprocesseur inséré dans son circuit électronique. Merci à Wikipedia |
Pour la microélectronique, le silicium polycristallin doit être converti en silicium monocristallin. On fond le matériau juste au-dessus de sa température de fusion, prêt à recristalliser si on abaisse la température. Plusieurs procédés existent. L'un d'eux consiste à introduire un germe, petit cristal monocristallin. La croissance cristalline se produit à partir de ce germe, au fur et à mesure que l'on retire le germe vers le haut tout en le faisant tourner à vitesse très lente.
Le barreau obtenu est ensuite tranché en rondelles fines (les galettes ou wafers). C'est sur ces galettes que sont gravés tous les composants d'un circuit intégré (puce) en petits carrés (die), par injection d'éléments chimiques sur des endroits précisément délimités par des masques. On peut ainsi graver jusqu'à mille puces sur une même galette. Elles sont séparées par découpage et enveloppées d'une protection (fig.33).
L'exemple des réseaux cristallins nous a montré qu'il est possible de remplir l'espace par des polyèdres identiques posés dans la même orientation les uns contre les autres. Ils s'ajustent les uns aux autres comme des briques et ne laissent aucun vide entre eux. Nous l'avons vérifié pour le cube, l'octaèdre tronqué, les dodécaèdres rhombique et rhombo-hexagonal.
Les mathématiciens ont recherché quelles étaient les formes possibles qui sont capables de remplir l'espace par empilement. Ce questionnement existe au moins depuis Aristote et n'a pas encore reçu de réponse exhaustive.
 Fig.7
Fig.7Nous pouvons par exemple nous demander s'il est possible de remplir l'espace avec des boules. La pratique montre que si nous serrons les boules les unes contre les autres, elles laissent entre elles de petits vides. Elles sont donc incapables de remplir l'espace complètement (fig.7). Si ces boules sont des oranges un peu molles et que nous les pressons assez fort pour les obliger à remplir les vides, nous les déformons. Leurs faces s'aplatissent contre celles de l'orange voisine. Finalement elles deviennent des polyèdres, volumes dont les faces sont plates.
On pourrait imaginer une sorte de boule qui serait bombée d'un côté et en creux de l'autre pour s'adapter à la boule voisine. Il y a donc des creux ou volumes concaves (mot de la famille de cave qui est un trou dans la terre), et des volumes convexes sans creux. Nous nous limitons ici aux polyèdres convexes, les volumes les plus simples.
Examinons tout d'abord les polyèdres réguliers. Un polyèdre est régulier s'il est constitué de faces toutes identiques et régulières (tous leurs côtés identiques), et que tous ses sommets sont identiques. Il n'existe que 5 polyèdres réguliers convexes: le tétraèdre (4 faces), le cube (ou hexaèdre) (6 faces), l'octaèdre (8 faces), le dodécaèdre (12 faces) et l'icosaèdre (20 faces). On les désigne sous le nom de solides de Platon.
Seul le cube a la propriété de remplir l'espace. Les autres laissent des vides entre eux. Toutefois, on pourra combler ces vides avec un autre type de polyèdre (voir plus loin).
D'autres polyèdres ont également des faces régulières, mais leur assemblage ne l'est pas. Ils sont composés de plusieurs types de faces associés, par exemple des losanges avec des carrés, ou, comme les ballons de football, des hexagones et des pentagones. Dans cette catégorie, on trouve les 13 solides d'Archimède.
Le mathématicien russe Fedorov a démontré qu'il n'existait que 5 polyèdres réguliers ou semi-réguliers (dont les sommets sont équivalents) capables de paver l'espace: le cube, l'octaèdre tronqué, le dodécaèdre rhombique, le dodécaèdre rhombo-hexagonal et le prisme hexagonal. On retrouve donc les polyèdres que nous connaissons déjà, plus le prisme hexagonal. On peut ajouter le prisme triangulaire et le gyrobifastigium (deux prismes triangulaires accolés), moins réguliers (fig.34).
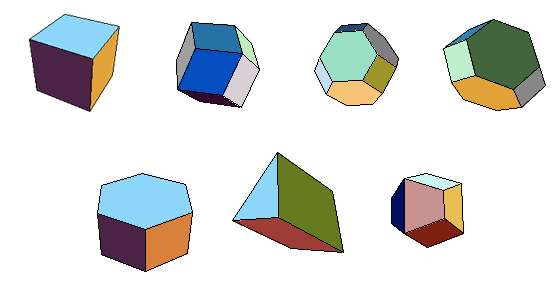
Fig.34- Les polyèdres les plus simples qui remplissent l'espace:
cube, dodécaèdre rhombique, octaèdre tronqué, dodécaèdre rhombo-hexagonal
prisme hexagonal, prisme triangulaire, gyrobifastigium. D'après Mathworld
A partir de ces polyèdres de base, beaucoup d'autres existent, obtenus par des déformations globales, par exemple le parallélépipède rectangle qui est un allongement du cube. On peut trouver des possibilités d'empilement multiples si on s'autorise à les placer dans des orientations différentes pour qu'ils s'emboitent.
Certains mathématiciens s'emploient à en faire le catalogue: sachant que d'autres polyèdres et méthodes d'assemblage peuvent toujours être découverts, ils ont répertorié 27 polyèdres à 6 faces, 16 à 7 faces, l'octaèdre, 26 à 10, 40 à 11, 16 à 12, 4 à 13, 8 à 14, 1 à 16, 2 à 17, 1 à 18, 6 à 20 (isocaèdre), 2 à 21, 5 à 22, 2 à 23, 1 à 24...Enfin, on peut associer 2 types de polyèdres et même plus afin de combler avec l'un les trous laissés par l'autre, comme cela a été fait plus haut avec le pavage de Penrose à deux dimensions où sont associés deux types de losanges.
Voici des combinaisons qui marchent:
Dans certains cas, la description de structures complexes de notre espace à 3 dimensions gagne beaucoup en simplicité lorsqu'on la décrit dans un espace de dimension supérieure ou super-espace. C'est le cas des cristaux apériodiques (quasi-cristaux, cristaux incommensurables) qui deviennent périodiques dans ces espaces.
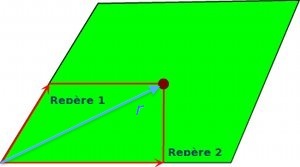
Fig.35- Un champ est une surface à deux dimensions. Pour indiquer la position d'un piquet dans ce champ, on doit fournir deux repères, par exemple ses distances par rapport à deux côtés.
D'où vient cette notion de dimension supérieure? La dimension (ou plus exactement la dimensionnalité - voir article Images fractales) peut être définie comme le nombre de coordonnées nécessaires pour préciser la position d'un élément (un point) de cette structure. Par exemple, une ligne est un espace à une seule dimension, car si on part d'un repère zéro sur cette ligne, il suffit d'indiquer la distance (dans un sens ou dans l'autre) par rapport à ce repère pour situer un point de cette ligne. De même dans un plan on peut indiquer la position d'un point en indiquant ses 2 coordonnées par rapport à deux axes de ce plan (fig.35). C'est un espace de dimensionnalité 2.
Si sur une ligne, donc un espace de dimension 1, on a une structure faite d'une succession de disques telle que celle de la figure 36a, il n'est pas simple de décrire simplement la position des disques.
Mais si dans ce cas particulier, on sépare ces disques en deux catégories (une verte et une bleue - fig.36b), alors on peut décrire séparément les disques bleus dans un espace avec une périodicité et les disques verts dans un autre espace avec une autre périodicité (fig.36c).
| Fig. 36a- Structure réelle à décrire |  | 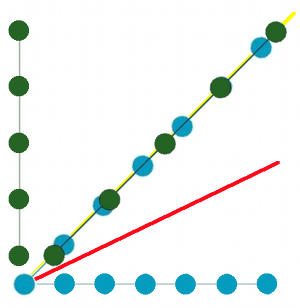 Fig.36d- Combinaison des 2 espaces et projection sur une droite |
| Fig.36b- Séparation en 2 catégories, verte et bleue |  | |
| Fig.36c- Séparation en 2 espaces. D'après F. Mompiou |  |
On a donc remplacé la structure à une dimension par la combinaison de deux variables (la position des disques bleus et celle des disques verts). Autrement dit, on est passé dans un espace à deux dimensions.
On peut alors imaginer cet espace plus vaste avec ses deux axes (fig.36d) dans lequel ces deux périodicités se combinent dans le plan (des structures non représentées sur la figure). Si on coupe cet espace par la ligne diagonale jaune, on retrouve notre structure de départ de 36b. On pourrait trouver d'autres combinaisons en coupant par d'autres lignes telles que la ligne rouge. Ce qui est à retenir, c'est que la structure réelle à une dimension dessinée sur cette ligne jaune peut-être définie comme la coupe (ou encore la projection) d'un espace à deux dimensions.
Dans les cristaux incommensurables, c'est de manière semblable que leurs diagrammes de diffraction, obtenus sur un cliché à 2 dimensions, peuvent être décrits avec 4 indices. On a donc la possibilité simple de les définir dans un espace de dimension 4. Le cristal lui-même de l'espace à 3 dimensions peut être défini dans un espace de 4, 5 ou 6 dimensions où il est alors périodique.
Le même artifice mathématique de super-espace a été utilisé dans le cas des quasi-cristaux. Bien que ces cristaux aient une réalité concrète dans notre espace à 3D en tant qu'empilement de motifs atomiques, A. Katz et M. Duneau, chercheurs de l'école Polytechnique (Paris) ont montré en 1985 qu'on pouvait les décrire de façon beaucoup plus simple dans un super-espace de 4 dimensions ou plus. On est ramené à la réalité concrète de troisième dimension en coupant ce super-espace par un volume à 3 dimensions ou en le projetant dans ce volume.
Par exemple, des quasi-cristaux (Al-Li-Cu) de symétrie icosaédrique peuvent être indexés par 6 coordonnées (pour plus de détail, voir le cours de S. Ravy). On coupe cet espace à 6 dimensions par un hyperplan à 3 dimensions pour retomber sur la structure réelle. L'intérêt de ce formalisme qui semble une complication est au contraire de décrire le quasi-cristal de façon beaucoup plus simple, car à 6 dimensions, il comporte des périodicités de translation semblables aux systèmes cristallins des cristaux ordinaires.
Nous allons donner une image concrète de ce que signifie couper un super-espace par un hyper-plan en prenant comme exemple un espace à 2 dimensions, donc un plan, dans lequel nous considérons une structure très simple pour notre exemple, deux cercles entrelacés (fig.37a). Il nous est possible de décrire précisément ces cercles en indiquant leurs centres, leurs rayons, etc.
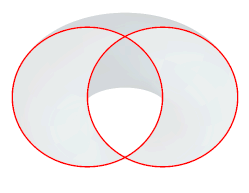 |  |
| Fig. 37a- Deux cercles entrelacés dans un plan | Fig.37b- Cercles obtenus par la coupe d'un tore par un plan (cercles de Villarceau) |
Mais alternativement, nous pouvons imaginer un espace de plus grande dimension sans réalité concrète du point de vue de ces cercles entrelacés, le super-espace à 3 dimensions. Dans cet espace, nous imaginons un tore, c'est-à-dire un anneau semblable à une bouée (fig. 37b). Un tore est une figure extrêmement simple parce qu'elle est régulière, symétrique, homogène.
Si on coupe le tore par un plan, on obtient des figures complexes qui varient selon l'inclinaison du plan. Dans une certaine position où le plan est tangent (il touche le tore - mot de la même famille que tangible) à la fois au-dessus d'un côté et au-dessous de l'autre, on obtient les deux cercles de la fig 37a (appelés par les mathématiciens cercles de Villarceau).
Dans le cadre de cet article, ce qui est important à retenir, c'est qu'on dispose d'une méthode pour décrire ces cercles dans un espace de dimension 3 alors qu'ils n'ont une réalité qu'en dimension 2. Cela peut faire apparaitre des symétries inapparentes autrement.
Bien entendu, dans ce cas, comme dans le cas des cristaux apériodiques, l'invention d'un super-espace est un artifice mathématique. On l'invente pour décrire une structure complexe parce qu'elle devient soudainement beaucoup plus simple et symétrique. Toutefois, cet artifice pourrait nous donner des idées sur la réalité d'un super-espace qu'au départ on suppose irréel. Pourrait-il être réel?
Au fond, que percevons-nous de notre réalité? Il se peut que la réalité de l'univers soit beaucoup plus vaste que ce que nous en percevons et que par constitution physique, nous soyons capables d'en percevoir seulement 3 dimensions. Or des scientifiques ont été amenés à imaginer un monde à plusieurs couches parallèles pour expliquer certains phénomènes quantiques. Mais alors ces mondes parallèles sont-ils seulement des artifices mathématiques? Ou bien ces réalités parallèles existent-elles? C'est la question que se posent certains physiciens quantiques. (voir Fondements de la physique quantique)
Article dans ce site
Autres articles
Minéraux (parfois avec cristallographie)
Cristallographie
Technologie
Géométrie
 . Je cite également ce site vraiment magique de Thérèse Eveilleau qui y a passé des milliers d'heures. On peut y voir des animations du pavage
d'une surface qui ont été réalisées avec beaucoup d'imagination.
. Je cite également ce site vraiment magique de Thérèse Eveilleau qui y a passé des milliers d'heures. On peut y voir des animations du pavage
d'une surface qui ont été réalisées avec beaucoup d'imagination.Texte conforme à la nouvelle orthographe française (1990)
1 mars 2011